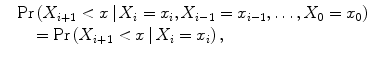Both X t and t Scales are Discrete
Example 1.2 (Bernoulli Process). Flipping a coin repeatedly (and indefinitely). In this case, X 1, X 2, X 3, are the individual outcomes (the state space consists of1 and 1, to be interpreted as losing or winning a dollar).
Example 1.3 (Cumulative Bernoulli Process). Consider the same Bernoulli process as in Example , where Y 1, Y 2, Y 3, now represent the cumulative sum of money won so far (i.e., Y 1= X 1,
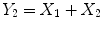
,
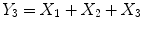
, ). This time the Y values are correlated (the state space consists of all integers).
Example 1.4 (Markov Chains). These will be studied extensively during the first part of the book (the sample space consists of a handful of integers for finite Markov chains and of all integers for infinite Markov chains).
X t Discrete, t Continuous
Example 1.5 (Poisson Process). The number of people who have entered a library from time zero until time t . X ( t ) will have a Poisson distribution with a mean of t ( being the average arrival rate), but the X are not independent (Fig. 6.1 for a graphical representation of one possible realization of such a process the sample space consists of all nonnegative integers).
Example 1.6 (Queuing Process). People not only enter but also leave a library (this is an example of an infinite-server queue; to fully describe the process, we need also the distribution of the time a visitor spends in the library). There are also queues with one server, two servers, etc., with all sorts of interesting variations.
Both X t and t Continuous
Example 1.7 (Brownian Motion). Also called diffusion a tiny particle suspended in a liquid undergoes an irregular motion due to being struck by the liquids molecules. We will study this in one dimension only, investigating issues such as, for example, the probability the particle will (ever) come back to the point from which it started.
X t Continuous, t Discrete
Example 1.8 (Time Series). Monthly fluctuations in the inflation rate, daily fluctuations in the stock market, and yearly fluctuations in the Gross National Product fall into the category of time series. One can investigate trends (systematic and seasonal) and design/test various models for the remaining (purely random) component (e.g., Markov, Yule). An important issue is that of estimating the models parameters.
In this book we investigate at least one type of each of the four categories, namely:
Finite Markov chains, branching processes, and the renewal process (4);
Poisson process, birth and death processes, and the continuous-time Markov chain (Chaps. 58);
Brownian motion ();
Autoregressive models ().
Solving such processes (for any finite selection of times t 1, t 2, , t N ) requires computing the distribution of each individual X ( t ), as well as the bivariate distribution of any X ( t 1), X ( t 2) pair, trivariate distribution of any X ( t 1), X ( t 2), X ( t 3) triplet, and so on. As the multivariate cases are usually simple extensions of the univariate one, the univariate distributions of a single X ( t ) will be the most difficult to compute.
Yet, depending on the type of process being investigated, the mathematical techniques required are surprisingly distinct. We require:
All aspects of matrix algebra and the basic theory of difference equations to handle finite Markov chains;
A good understanding of function composition and the concept of a sequence-generating function to deal with branching processes and the renewal theory;
A basic (at least conceptually) knowledge of partial differential equations (for );
Familiarity with eigenvalues of a square matrix to learn how to compute a specific function of any such matrix (for ); and, finally
Calculus ().
In an effort to make the book self-contained,we provide a brief overview of each of these mathematical tools in the chapter appendices.
We conclude this section with two definitions:
Definition 1.1 (Stationary).
A process is stationary when all the X t have the same distribution,and also: for each ,all the ( X t , X t +) pairs have the same bivariate distribution,similarly for triplets,etc.
Example 1.9. Our queueing process can be expected to become stationary (at least in the t limit,i.e., asymptotically),but the cumulative-sum process is nonstationary.
Definition 1.2 (Markovian property) .
A process is Markovian when
or, more generally, to compute the probability of an event in the future, given a knowledge of the past and present,one can discard information about the past without affecting the answer. This does not imply X i +1 is independent of,for example X i 1, X i 2.
Example 1.10. The stock market is most likely non-Markovian (trends), whereas the cumulative-sum process has a Markovian property.
The main objective in solving a specific stochastic-process model is to find the joint distribution of the processs values for any finite selection of the t indices. The most basic and important of these is the univariate distribution of X t , for any value of t , from which the multivariate distribution of several X t (usually) easily follows.













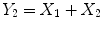 ,
, 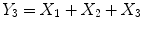 , ). This time the Y values are correlated (the state space consists of all integers).
, ). This time the Y values are correlated (the state space consists of all integers).