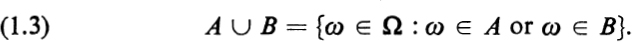Erhan Cinlar - Introduction to Stochastic Processes

EHRAN INLAR

Norman J. Sollenberger Professor in Engineering
Princeton University

DOVER PUBLICATIONS, INC.
Mineola, New York

Copyright

Copyright 1975 by Erhan inlar

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2013, is an unabridged republication of the work originally published in 1975 by Prentice-Hall, Inc., Englewood Cliffs, New Jersey.

Library of Congress Cataloging-in-Publication Data
inlar, E. (Erhan), 1941

Introduction to stochastic processes / Erhan inlar. Dover edition.

pages cm.

Summary: This clear presentation of the most fundamental models of random phenomena employs methods that recognize computer-related aspects of theory. Topics include probability spaces and random variables, expectations and independence, Bernoulli processes and sums of independent random variables, Poisson processes, Markov chains and processes, and renewal theory. Includes an introduction to basic stochastic processes. 1975 edition Provided by publisher.

Includes bibliographical references and index.

eISBN-13: 978-0-486-27632-8

1. Stochastic processes. I. Title.

A274.C56 2013
519.23dc23

2012028204

Manufactured in the United States by Courier Corporation
49797601
www.doverpublications.com

A man wanted to dock the tail of his horse. He consulted a wise man on how short to make it. Make it as short as it pleases you, said the wise man, for, no matter what you do, some will say it is too long, some too short, and your opinion itself will change from time to time.

This book is an introduction to stochastic processes. It covers most of the basic processes of interest except for two glaring omissions. Topics covered are developed in some depth, some fairly recent results are included, and references are given for further reading. These features should make the book useful to scientists and engineers looking for models and results to use in their work. However, this is primarily a textbook; a large number of numerical examples are worked out in detail, and the exercises at the end of each chapter are there to illustrate the theory rather than to extend it.

When theorems are proved, this is done in some detail; even the ill-prepared student should be able to follow them. On the other hand, not all theorems are proved. If a result is of sufficient intrinsic interest, and if it can be explained and understood, then it is listed as a theorem even though it could not be proved with the elementary tools available in this book. This freedom made it possible to include two characterization theorems on Poisson processes, several limit theorems on the ratios of additive functionals of Markov processes, several results on the sample path behavior of (continuous parameter) Markov processes, and a large number of results dealing with stopping times and the strong Markov property.

The book assumes a background in calculus but no measure theory; thus, the treatment is elementary. At the same time, it is from a modern viewpoint. In the modern approach to stochastic processes, the primary object is the behavior of the sample paths. This is especially so for the applied scientist and the engineer, since it is the sample path which he observes and tries to control. Our approach capitalizes on this happy harmony between the methods of the better mathematician and the intuition of the honest engineer.

We have also followed the modern trends in preferring matrix algebra and recursive methods to transform methods. The early probability theorists desire to cast his problem into one concerning distribution functions and Fourier transforms is understandable in view of his background in classical analysis and the notion of an acceptable solution prevailing then. The present generation, however, influenced especially by the availability of computers, prefers a characterization of the solution coupled with a recursive method of obtaining it to an explicit closed form expression in terms of the generating functions of the Laplace transforms of the quantities of actual interest.

The first part of the book is based on a set of lecture notes which were used by myself and several colleagues in a variety of applied courses on stochastic processes over the last five years. In that stage I was helped by P. A. Jacobs and C. G. Gilbert in collecting problems and abstracting papers from the applied literature. Most of the final version was written during my sabbatical stay at Stanford University; I should like to thank the department of Operations Research for their hospitality then. While there I have benefited from conversations with K. L. Chung and D. L. Iglehart; it is a pleasure to acknowledge my debt to them. I am especially indebted to A. F. Karr for his help throughout this project; he eliminated many inaccuracies and obscurities. I had the good fortune to have G. Lemmond to type the manuscript, and finally, the National Science Foundation to support my work.

E. INLAR

The theory of probability now constitutes a formidable body of knowledge of great mathematical interest and of great practical importance. It has applications in every area of natural science: in minimizing the unavoidable errors of observations, in detecting the presence of assignable causes in observed phenomena, and in discovering the basic laws obscured by chance variations. It is also an indispensable tool in engineering and business: in deducing the true lessons from statistics, in forecasting the future, and in deciding which course to pursue.

In this chapter the basic vocabulary of probability theory will be introduced. Most of these terms have cognates in ordinary language, and the reader should do well not to fall into a false sense of security because of his previous familiarity with them. Instead he should try to refine his own use of these terms and watch for the natural context within which each term appears.

The basic notion in probability theory is that of a random experiment: an experiment whose outcome cannot be determined in advance. The set of all possible outcomes of an experiment is called the sample space of that experiment.

An event is a subset of a sample space. An event A is said to occur if and only if the observed outcome of the experiment is an element of the set A.

(1.1) EXAMPLE. Consider an experiment that consists of counting the number of traffic accidents at a given intersection during a specified time interval. The sample space is the set {0, 1, 2, 3,...}. The statement the number of accidents is less than or equal to seven describes the event {0, 1,..., 7}. The event A = {5, 6, 7,...} occurs if and only if the number of accidents is 5 or 6 or 7 or....

Given a sample space and an event A, the complement Ac of A is defined to be the event which occurs if and only if A does not occur, that is,

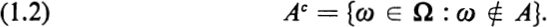
Given two events A and B, their union is the event which occurs if and only if either A or B (or both) occurs, that is,