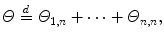Andreas E. Kyprianou - Fluctuations of Lévy Processes with Applications: Introductory Lectures
Here you can read online Andreas E. Kyprianou - Fluctuations of Lévy Processes with Applications: Introductory Lectures full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Fluctuations of Lévy Processes with Applications: Introductory Lectures
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Fluctuations of Lévy Processes with Applications: Introductory Lectures: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Fluctuations of Lévy Processes with Applications: Introductory Lectures" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Lvy processes are the natural continuous-time analogue of random walks and form a rich class of stochastic processes around which a robust mathematical theory exists. Their application appears in the theory of many areas of classical and modern stochastic processes including storage models, renewal processes, insurance risk models, optimal stopping problems, mathematical finance, continuous-state branching processes and positive self-similar Markov processes.
This textbook is based on a series of graduate courses concerning the theory and application of Lvy processes from the perspective of their path fluctuations. Central to the presentation is the decomposition of paths in terms of excursions from the running maximum as well as an understanding of short- and long-term behaviour.
The book aims to be mathematically rigorous while still providing an intuitive feel for underlying principles. The results and applications often focus on the case of Lvy processes with jumps in only one direction, for which recent theoretical advances have yielded a higher degree of mathematical tractability.
The second edition additionally addresses recent developments in the potential analysis of subordinators, Wiener-Hopf theory, the theory of scale functions and their application to ruin theory, as well as including an extensive overview of the classical and modern theory of positive self-similar Markov processes. Each chapter has a comprehensive set of exercises.
Andreas E. Kyprianou: author's other books
Who wrote Fluctuations of Lévy Processes with Applications: Introductory Lectures? Find out the surname, the name of the author of the book and a list of all author's works by series.














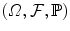 is said to be a Brownian motion if the following hold:
is said to be a Brownian motion if the following hold: 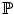 -almost surely continuous.
-almost surely continuous.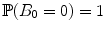 .
.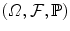 , is said to be a Poisson process with intensity >0 if the following hold:
, is said to be a Poisson process with intensity >0 if the following hold:  -almost surely right-continuous with left limits.
-almost surely right-continuous with left limits.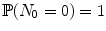 .
.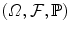 , is said to be a Lvy process if it possesses the following properties:
, is said to be a Lvy process if it possesses the following properties: 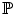 -almost surely right-continuous with left limits.
-almost surely right-continuous with left limits.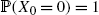 .
.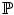 (with associated expectation operator
(with associated expectation operator 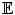 ) to be implicitly understood as its law.
) to be implicitly understood as its law.