Pierre Brémaud - Fourier Analysis and Stochastic Processes
Here you can read online Pierre Brémaud - Fourier Analysis and Stochastic Processes full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Fourier Analysis and Stochastic Processes
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Fourier Analysis and Stochastic Processes: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Fourier Analysis and Stochastic Processes" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This work is unique as it provides a uniform treatment of the Fourier theories of functions (Fourier transforms and series, z-transforms), finite measures (characteristic functions, convergence in distribution), and stochastic processes (including arma series and point processes).
It emphasises the links between these three themes. The chapter on the Fourier theory of point processes and signals structured by point processes is a novel addition to the literature on Fourier analysis of stochastic processes. It also connects the theory with recent lines of research such as biological spike signals and ultrawide-band communications.
Although the treatment is mathematically rigorous, the convivial style makes the book accessible to a large audience. In particular, it will be interesting to anyone working in electrical engineering and communications, biology (point process signals) and econometrics (arma models).
A careful review of the prerequisites (integration and probability theory in the appendix, Hilbert spaces in the first chapter) make the book self-contained. Each chapter has an exercise section, which makes Fourier Analysis and Stochastic Processes suitable for a graduate course in applied mathematics, as well as for self-study.
Pierre Brémaud: author's other books
Who wrote Fourier Analysis and Stochastic Processes? Find out the surname, the name of the author of the book and a list of all author's works by series.














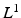 and
and 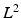 , but also z-transforms which are the backbone of discrete-time signal processing together with the notion of (time- invariant) linear filtering. We spend some time with the famous Poisson summation formulathe bridge between Fourier transforms and Fourier serieswhich is intimately connected to the celebrated ShannonNyquist sampling theorem of signal processing and is of special interest to physicists and engineers in that it justifies the calculations involving the Dirac train of impulses without recourse to distribution theory. For the
, but also z-transforms which are the backbone of discrete-time signal processing together with the notion of (time- invariant) linear filtering. We spend some time with the famous Poisson summation formulathe bridge between Fourier transforms and Fourier serieswhich is intimately connected to the celebrated ShannonNyquist sampling theorem of signal processing and is of special interest to physicists and engineers in that it justifies the calculations involving the Dirac train of impulses without recourse to distribution theory. For the 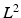 Fourier theory of functions and sequences, some background in Hilbert spaces is required. The results obtained, such as the orthogonal projection theorem, the isometric extension theorem and the orthonormal basis theorem, will be recurrently used in the rest of the book.
Fourier theory of functions and sequences, some background in Hilbert spaces is required. The results obtained, such as the orthogonal projection theorem, the isometric extension theorem and the orthonormal basis theorem, will be recurrently used in the rest of the book.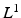
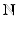 ,
, 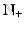 and
and 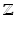 . The sets of real numbers, non-negative real numbers and complex numbers are denoted respectively by
. The sets of real numbers, non-negative real numbers and complex numbers are denoted respectively by 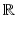 ,
, 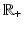 and
and 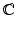 .
.
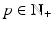 ,
, 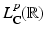 denotes the collection of measurable functions
denotes the collection of measurable functions 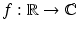 such that
such that 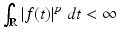 . Similarly, for all intervals
. Similarly, for all intervals 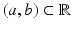 ,
, 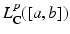 denotes the collection of measurable functions
denotes the collection of measurable functions 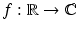 such that
such that 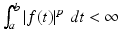 . A function
. A function 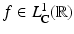 is called integrable (with respect to Lebesgue measure). A function
is called integrable (with respect to Lebesgue measure). A function 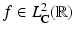 is called square-integrable (with respect to Lebesgue measure).
is called square-integrable (with respect to Lebesgue measure). 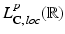 is, by definition, the set of functions
is, by definition, the set of functions 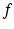 that are in
that are in 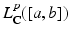 for all intervals
for all intervals 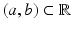 . A function
. A function 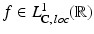 is said to be locally integrable. Similar definitions and notation will be used for functions
is said to be locally integrable. Similar definitions and notation will be used for functions 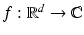 when
when 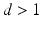 .
.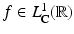 is the function
is the function 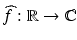 defined by:
defined by: 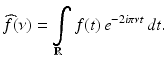
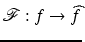 or more simply,
or more simply, 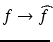 , whenever the context is unambiguous.
, whenever the context is unambiguous.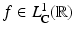 is bounded and uniformly continuous.
is bounded and uniformly continuous.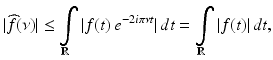
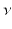 and is finite. Also, for all
and is finite. Also, for all 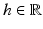 ,
, 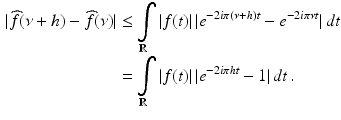
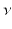 and tends to
and tends to