Vaclav E. Benes - General Stochastic Processes in the Theory of Queues
Here you can read online Vaclav E. Benes - General Stochastic Processes in the Theory of Queues full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: Dover Publications, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:General Stochastic Processes in the Theory of Queues
- Author:
- Publisher:Dover Publications
- Genre:
- Year:2017
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
- 100
- 1
- 2
- 3
- 4
- 5
General Stochastic Processes in the Theory of Queues: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "General Stochastic Processes in the Theory of Queues" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
General Stochastic Processes in the Theory of Queues — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "General Stochastic Processes in the Theory of Queues" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
STOCHASTIC
PROCESSES
IN THE
THEORY
OF
QUEUES
Identifiers: LCCN 2017013597| ISBN 9780486820309 | ISBN 0486820300 Subjects: LCSH: Queuing theory. | Stochastic processes. Classification: LCC QA273 .B45 2017 | DDC 519.8/2dc23 LC record available at https://lccn.loc.gov/2017013597 Manufactured in the United States by LSC Communications
82030001 2017
www.doverpublications.com
In this monograph I attempt such a task for the topic of delays in queueing systems with one server. Delays in queues with one server and order of arrival service are considered without any restrictions on the statistical character of the offered traffic. Elementary methods establish formulas and equations describing probabilities of delay. These methods de-emphasize special statistical models and yield a general theory. In spite of the generality of this approach, intuitive proofs and extensive explanations of the physical significance of formulas are given, as well as rigorous derivations. The theory is applied to specific models to obtain illustrative new results.
Under mild conditions of stationarity, the asymptotic behavior in time of the delay is studied and is shown to be governed by a functional equation closely analogous to the fundamental equation of branching processes, already used in special queueing models. A generalization of the Pollaczek-Khinchin formula is derived for the case in which delays do not build up. So many monographs, surveys, and books on the theory of queues are currently appearing that I have made no effort to canvass the vast extant literature of queueing. References to it have been included only insofar as they arose naturally in the text. For the benefit of the reader, therefore, I cite the following books: J. D. R. Cox and W. L. L.
Smith, Queues. New York: John Wiley and Sons, 1961. T. L. Saaty, Elements of Queueing Theory. New York: McGraw-Hill Book Co., 1961. L. Takcs, Introduction to the Theory of Queues. New York: Oxford University Press, 1962.
I would like to express my gratitude to Bell Telephone Laboratories for providing a milieu in which advanced theoretical work on practical topics can be pursued, and for supplying all the secretarial work involved in completion of the manuscript. Also, it is a pleasure to acknowledge that a careful reading of the manuscript by my colleague E. Wolman resulted in many corrections and improvements. Murray Hill, New Jersey V. E. November 5, 1962.
INTRODUCTION
These results concern general stochastic processes in the theory of queues with one server and order-of-arrival service. In this work we have three aims: both new and known. What follows is written only partly as a contribution to the mathematical analysis of congestion. It is also, at least initially, a frankly tutorial account aimed at increasing the public understanding of congestion by first steering attention away from special statistical models, and obtaining a general theory. Such a point of view, it is hoped, will yield new methods in problems other than congestion. When a general theory can be given, it will be useful in several ways.
It will (i) increase our understanding of complex systems; (ii) yield new specific results, curves, tables, etc; and (iii) extend theory to cover interesting cases which are known to be inadequately described by existing results. At first acquaintance, the theorems of such a general theory may not resemble results at all; that is, they may not seem to be facts which one could obviously and easily use to solve a real problem. A general theory is really a tool or principle, expressing the essence or structure of a system; properly explained and used, this tool will yield formulas and other specifics with which problems can be treated.
As a mathematical idealization of the delays to be suffered in the system, we use the virtual waiting-time W(t), which can be defined as the time a customer would have to wait for service if he arrived at time t. W() is continuous from the left; at epochs of arrival of customers, W() jumps upward discontinuously by an amount equal to the service-time of the arriving customer; otherwise W() has slope 1 while it is positive. If it reaches zero, it stays equal to zero until the next jump. It is usual to define the stochastic process W() in terms of the arrival epoch tk and the service-time. Sk of the kth arriving customer, for k = 1, 2, . However, the following procedure is a little more elegant; we describe the service-times and the arrival epochs simultaneously by a single function K(), which is defined for t 0, left-continuous, nondecreasing, and constant between successive jumps.
The locations of the jumps are the epochs of arrivals, and the magnitudes are the service-times. It is convenient . 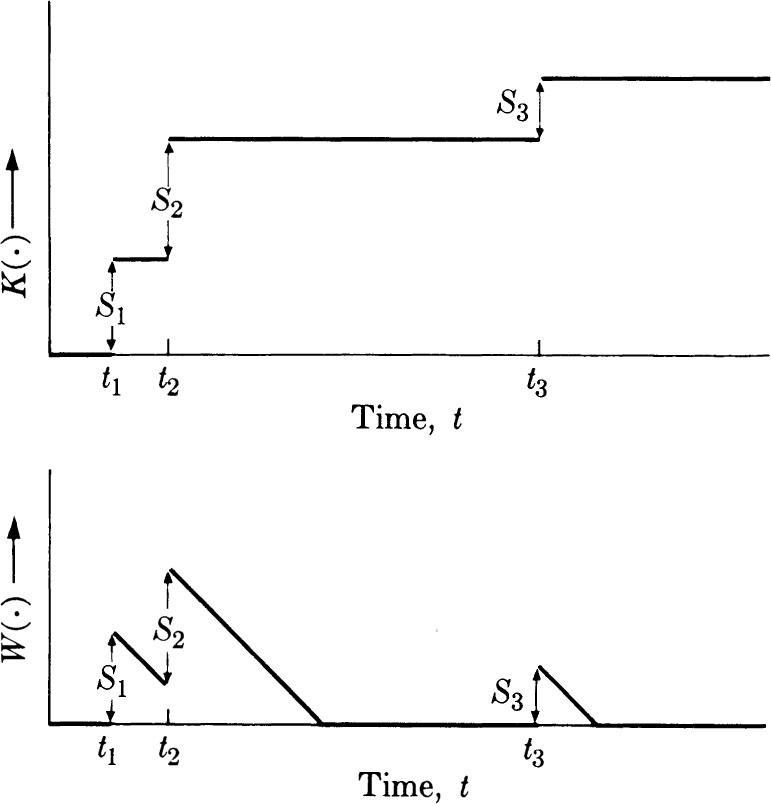
Font size:
Interval:
Bookmark:
Similar books «General Stochastic Processes in the Theory of Queues»
Look at similar books to General Stochastic Processes in the Theory of Queues. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book General Stochastic Processes in the Theory of Queues and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.




![Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c](/uploads/posts/book/193156/thumbs/d-bicki-krzysztof-queues-and-l-vy-fluctuation.jpg)








