Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c
Here you can read online Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, year: 2015, publisher: Springer International Publishing, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
![Dębicki Krzysztof Queues and Lévy Fluctuation Theory [recurso electrónico] $c](https://litark.com/uploads/posts/book/193156/d-bicki-krzysztof-queues-and-l-vy-fluctuation.jpg)
- Book:Queues and Lévy Fluctuation Theory [recurso electrónico] $c
- Author:
- Publisher:Springer International Publishing
- Genre:
- Year:2015
- City:Cham
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Queues and Lévy Fluctuation Theory [recurso electrónico] $c: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Queues and Lévy Fluctuation Theory [recurso electrónico] $c" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
The book provides an extensive introduction to queueing models driven by Lvy-processes as well as a systematic account of the literature on Lvy-driven queues. The objective is to make the reader familiar with the wide set of probabilistic techniques that have been developed over the past decades, including transform-based techniques, martingales, rate-conservation arguments, change-of-measure, importance sampling, and large deviations. On the application side, it demonstrates how Lvy traffic models arise when modelling current queueing-type systems (as communication networks) and includes applications to finance. Queues and Lvy Fluctuation Theory will appeal to graduate/postgraduate students and researchers in mathematics, computer science, and electrical engineering. Basic prerequisites are probability theory and stochastic processes.;Introduction -- Lvy processes and Lvy-driven queues -- Steady-state workload -- Transient workload -- Heavy traffic -- Busy period -- Workload correlation function -- Stationary workload asymptotics -- Transient asymptotics -- Simulation of Lvy-driven queues -- Variants of the standard queue -- Lvy-driven tandem queues -- Lvy-driven queueing networks -- Applications in communication networks -- Applications in mathematical finance -- Computational aspects: inversion techniques -- Concluding remarks -- Bibliography.
Dębicki Krzysztof: author's other books
Who wrote Queues and Lévy Fluctuation Theory [recurso electrónico] $c? Find out the surname, the name of the author of the book and a list of all author's works by series.
![Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c](/uploads/posts/book/193156/thumbs/d-bicki-krzysztof-queues-and-l-vy-fluctuation.jpg)
Dębicki Krzysztof
Christos G. Cassandras
Jorge Navarro
Sheldon M. Ross
Vaclav E. Benes
Nicolas Lanchier
Andreas E. Kyprianou
Pierre Brémaud
Donald Gross
Queues and Lévy Fluctuation Theory [recurso electrónico] $c — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Queues and Lévy Fluctuation Theory [recurso electrónico] $c" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Springer International Publishing Switzerland 2015
Krzysztof Dbicki and Michel Mandjes Queues and Lvy Fluctuation Theory Universitext 10.1007/978-3-319-20693-6_11. Introduction
Krzysztof Dbicki 1 and Michel Mandjes 2
(1)
Mathematical Institute, University of Wrocaw, Wrocaw, Poland
(2)
Korteweg-de Vries Institute for Mathematics, University of Amsterdam, Amsterdam, The Netherlands
The class of Lvy processes consists of all stochastic processes with stationary and independent increments; here stationarity means that increments corresponding to a fixed time interval are identically distributed, whereas independence refers to the property that increments corresponding to non-overlapping time intervals behave statistically independently. As such, Lvy processes cover several well-studied processes (e.g. Brownian motions and Poisson processes), but also, as this book will show, a wide variety of other processes, with their own specific properties in terms of their path structure. The process increments being stationary and independent, Lvy processes can be seen as the genuine continuous-time counterpart of the random walk 
, with independent and identically distributed Y i .
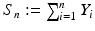
, with independent and identically distributed Y i .Lvy processes owe their popularity to their mathematically attractive properties as well as their wide applicability: they play an increasingly important role in a broad spectrum of application domains, ranging from finance to biology. Lvy processes were named after the French mathematician Paul Lvy (18861971), who played a pioneering role in the systematic analysis of processes with stationary and independent increments. A brief account of the history of Lvy processes (initially simply known as processes with stationary and independent increments) and its application fields is given in e.g. Applebaum [].
Application areas In mathematical finance , Lvy processes are being used intensively to analyze various phenomena. They are for instance suitable when studying credit risk, or for option pricing purposes (see e.g. Cont and Tankov []). An attractive feature of Lvy processes, particularly with applications in finance in mind, is that this class is rich in terms of possible path structures: it is perhaps the simplest class of processes that allows sample paths to have continuous parts interspersed with jumps at random epochs.
Another important application domain lies in operations research (OR). According to the functional central limit theorem, under mild conditions on the distribution of the increments, a scaled version of discrete-time random walks converges weakly to a Brownian motion. In line with this convergence, one can argue that under a suitable scaling and regularity conditions, there is weak convergence of classical GI/G/1 queueing systems (with discrete customers) to a queue with Brownian input, usually referred to as reflected Brownian motion [].
A more specific example, in which the limiting process is not necessarily Brownian motion, relates to the performance analysis of resources in communication networks. In the mid-1990s it was observed that the distribution of the sizes of documents transferred over the internet is heavy tailed : the complementary distribution of the document sizes decays roughly hyperbolically with a tail index such that the mean document size exists, but the corresponding variance is infinite. This entails that under particular conditions the aggregate of traffic generated by many users weakly converges to fractional Brownian motion, but under other conditions there is weak convergence to (a specific class of) Lvy processes (i.e. -stable Lvy motions); see Mikosch et al. []. In the latter regime, the performance of the network element can be evaluated by analyzing a queue fed by Lvy input.
Relevance of Lvy-driven queues; their construction; fluctuation theory The above OR-related considerations underscore the importance of analyzing queues with Lvy input (or Lvy-driven queues ). It should be noticed, though, that it is not a priori clear what should be understood by such a queue: for instance, in the case that the Lvy process under consideration is a Brownian motion, the input process is not increasing, nor is even a difference of increasing functions (i.e. it is not of finite variation), and therefore the corresponding queue cannot be seen as a storage system in the classical sense. Relying on a description of the queue as the solution of a so-called Skorokhod problem []. It is stressed that queues of the classical M/G/1 type (i.e. Poisson arrivals, generally distributed jobs, one server) fit in the framework of Lvy-driven queues. A Lvy-driven queue is also referred to as a Lvy process reflected at 0 , or a regulated Lvy process.
Interestingly, although queues are seemingly absent in the finance applications that we mentioned above, Lvy-driven queues are, in disguise, used intensively in that context as well. The reason for this is that many queueing-related metrics can be expressed in terms of extreme values attained by the driving (i.e. non-reflected) Lvy process. Precisely this knowledge about extremes, a body of results usually referred to as fluctuation theory , plays a pivotal role in finance; think for instance, in an insurance context, of the analysis of ruin probabilities, but also of techniques to price various exotic options and to quantify the corresponding sensitivities.
Goal of the book Having defined Lvy-driven queues, all questions that have been studied for classical queues now have their Lvy counterpartthe high-level goal of this book is to address these issues. For instance, a first question relates to the distribution of the steady-state workload of the queue: imposing the obvious stability criterion, can we explicitly characterize the stationary workload distribution? A second branch of questions relate to the impact of the initial workload; there the focus lies on determining the queues transient workload, but also various alternative transience-related metrics (such as the busy period and the correlation of the workload process) can be considered. In addition, just as in the world of classical queues, one can think of a variety of variants of the standard Lvy-driven queue: queues with a finite buffer, queues whose input characteristics are affected by the current workload level (feedback), queues with vacations and service interruptions, and Lvy-driven polling models. Finally, under specific conditions on the Lvy processes involved, one can let the output of a queue serve as the input for the next queue, and in this way we arrive at the notion of Lvy-driven queueing networks.
The objective of this textbook is to give a systematic account of the literature on Lvy-driven queues. In addition, we also intend to make the reader familiar with the wide set of techniques that has been developed over the past decades. In this survey, techniques that are highlighted include transform-based methods, martingales, rate-conservation arguments, change of measure, importance sampling, large deviations, and numerical inversion.
Complementary reading A few words on additional recommended literature. In the first place there are the textbooks by Bertoin [] provide brief introductions to Lvy-driven queues.
Organization Our book is organized as follows. Chapters with a description of numerical techniques. In more detail, the topics addressed in this monograph are the following.
Chapter formalizes the notion of Lvy-driven queues ; it is argued how in general queues can be defined without assuming that the input process is necessarily non-decreasing. We also define the special class of spectrally one-sided Lvy inputs, that is, Lvy processes with either only positive jumps or only negative jumps; we will extensively rely on this notion throughout the survey. In addition, this chapter introduces the class of -stable Lvy motions.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Similar books «Queues and Lévy Fluctuation Theory [recurso electrónico] $c»
Look at similar books to Queues and Lévy Fluctuation Theory [recurso electrónico] $c. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Christos G. Cassandras
Jorge Navarro
Sheldon M. Ross
Vaclav E. Benes
Nicolas Lanchier
Andreas E. Kyprianou
Pierre Brémaud
Donald Gross
Reviews about «Queues and Lévy Fluctuation Theory [recurso electrónico] $c»
Discussion, reviews of the book Queues and Lévy Fluctuation Theory [recurso electrónico] $c and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.