Numerical Analysis
Copyright 2011 by Princeton University Press
Published by Princeton University Press, 41 William Street,
Princeton, New Jersey 08540
In the United Kingdom: Princeton University Press, 6 Oxford Street,
Woodstock, Oxfordshire OX20 1TW
press.princeton.edu
All Rights Reserved
Library of Congress Control Number: 2010943322
ISBN: 978-0-691-14686-7
British Library Cataloging-in-Publication Data is available
The publisher would like to acknowledge the author of this volume for typesetting this book using LaTeX and Dr. Janet Englund and Peter Scott for providing the cover photograph
Printed on acid-free paper
Printed in the United States of America
10 9 8 7 6 5 4 3 2 1

Dedication
To the memory of Ed Conway who, along with his colleagues at Tulane University, provided a stable, adaptive, and inspirational starting point for my career.
Edward Daire Conway, III (19371985) was a student of Eberhard Friedrich Ferdinand Hopf at the University of Indiana. Hopf was a student of Erhard Schmidt and Issai Schur.

Contents

Preface
by faith and faith alone, embrace, believing where we cannot prove, from In Memoriam by Alfred Lord Tennyson, a memorial to Arthur Hallum.
Numerical analysis provides the foundations for a major paradigm shift in what we understand as an acceptable answer to a scientific or technical question. In classical calculus we look for answers like 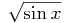 , that is, answers composed of combinations of names of functions that are familiar. This presumes we can evaluate such an expression as needed, and indeed numerical analysis has enabled the development of pocket calculators and computer software to make this routine. But numerical analysis has done much more than this. We will see that far more complex functions, defined, e.g., only implicitly, can be evaluated just as easily and with the same technology. This makes the search for answers in classical calculus obsolete in many cases. This new paradigm comes at a cost: developing stable, convergent algorithms to evaluate functions is often more difficult than more classical analysis of these functions. For this reason, the subject is still being actively developed. However, it is possible to present many important ideas at an elementary level, as is done here.
, that is, answers composed of combinations of names of functions that are familiar. This presumes we can evaluate such an expression as needed, and indeed numerical analysis has enabled the development of pocket calculators and computer software to make this routine. But numerical analysis has done much more than this. We will see that far more complex functions, defined, e.g., only implicitly, can be evaluated just as easily and with the same technology. This makes the search for answers in classical calculus obsolete in many cases. This new paradigm comes at a cost: developing stable, convergent algorithms to evaluate functions is often more difficult than more classical analysis of these functions. For this reason, the subject is still being actively developed. However, it is possible to present many important ideas at an elementary level, as is done here.
Today there are many good books on numerical analysis at the graduate level, including general texts [47, 134] as well as more specialized texts. We reference many of the latter at the ends of chapters where we suggest further reading in particular areas. At a more introductory level, the recent trend has been to provide texts accessible to a wide audience. The book by Burden and Faires [28] has been extremely successful. It is a tribute to the importance of the field of numerical analysis that such books and others [131] are so popular. However, such books intentionally diminish the role of advanced mathematics in the subject of numerical analysis. As a result, numerical analysis is frequently presented as an elementary subject. As a corollary, most students miss exposure to numerical analysis as a mathematical subject. We hope to provide an alternative.
Several books written some decades ago addressed specifically a mathematical audience, e.g., [80, 84, 86]. These books remain valuable references, but the subject has changed substantially in the meantime.
We have intentionally introduced concepts from various parts of mathematics as they arise naturally. In this sense, this book is an invitation to study more deeply advanced topics in mathematics. It may require a short detour to understand completely what is being said regarding operator theory in infinite-dimensional vector spaces or regarding algebraic concepts like tensors and flags. Numerical analysis provides, in a way that is accessible to advanced undergraduates, an introduction to many of the advanced concepts of modern analysis.
We have assumed that the general style of a course using this book will be to prove theorems. Indeed, we have attempted to facilitate a Moore method style of learning by providing a sequence of steps to be verified as exercises. This has also guided the set of topics to some degree. We have tried to hit the interesting points, and we have kept the list of topics covered as short as possible. Completeness is left to graduate level courses using the texts we mention at the end of many chapters.
The prerequisites for the course are not demanding. We assume a sophisticated understanding of real numbers, including compactness arguments. We also assume some familiarity with concepts of linear algebra, but we include derivations of most results as a review. We have attempted to make the book self-contained. Solutions of many of the exercises are provided.
About the name: the term numerical analysis is fairly recent. A classic book [170] on the topic changed names between editions, adopting the numerical analysis title in a later edition [171]. The origins of the part of mathematics we now call analysis were all numerical, so for millennia the name numerical analysis would have been redundant. But analysis later developed conceptual (non-numerical) paradigms, and it became useful to specify the different areas by names.
There are many areas of analysis in addition to numerical, including complex, convex, functional, harmonic, and real. Some areas, which might have been given such a name, have their own names (such as probability, instead of random analysis). There is not a line of demarcation between the different areas of analysis. For example, much of harmonic analysis might be characterized as real or complex analysis, with functional analysis playing a role in modern theories. The same is true of numerical analysis, and it can be viewed in part as providing motivation for further study in all areas of analysis.
The subject of numerical analysis has ancient roots, and it has had periods of intense development followed by long periods of consolidation. In many cases, the new developments have coincided with the introduction of new forms of computing machines. For example, many of the basic theorems about computing solutions of ordinary differential equations were proved soon after desktop adding machines became common at the turn of the 20th century. The emergence of the digital computer in the mid-20th century spurred interest in solving partial differential equations and large systems of linear equations, as well as many other topics. The advent of parallel computers similarly stimulated research on new classes of algorithms. However, many fundamental questions remain open, and the subject is an active area of research today.
All of analysis is about evaluating limits. In this sense, it is about infinite objects, unlike, say, some parts of algebra or discrete mathematics. Often a key step is to provide uniform bounds on infinite objects, such as operators on vector spaces. In numerical analysis, the infinite objects are often sets of algorithms which are themselves finite in every instance. The objective is often to show that the algorithms are well-behaved uniformly and provide, in some limit, predictable results.
In numerical analysis there is sometimes a cultural divide between courses that emphasize theory and ones that emphasize computation. Ideally, both should be intertwined, as numerical analysis could well be called computational analysis because it is the analysis of computational algorithms involving real numbers. We present many computational algorithms and encourage computational exploration. However, we do not address the subject of software development (a.k.a., programming). Strictly speaking, programming is not required to appreciate the material in the book. However, we encourage mathematics students to develop some experience in this direction, as writing a computer program is quite similar to proving a theorem. Computer systems are quite adept at finding flaws in ones reasoning, and the organization required to make software readable provides a useful model to follow in making complex mathematical arguments understandable to others.
Next page









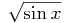 , that is, answers composed of combinations of names of functions that are familiar. This presumes we can evaluate such an expression as needed, and indeed numerical analysis has enabled the development of pocket calculators and computer software to make this routine. But numerical analysis has done much more than this. We will see that far more complex functions, defined, e.g., only implicitly, can be evaluated just as easily and with the same technology. This makes the search for answers in classical calculus obsolete in many cases. This new paradigm comes at a cost: developing stable, convergent algorithms to evaluate functions is often more difficult than more classical analysis of these functions. For this reason, the subject is still being actively developed. However, it is possible to present many important ideas at an elementary level, as is done here.
, that is, answers composed of combinations of names of functions that are familiar. This presumes we can evaluate such an expression as needed, and indeed numerical analysis has enabled the development of pocket calculators and computer software to make this routine. But numerical analysis has done much more than this. We will see that far more complex functions, defined, e.g., only implicitly, can be evaluated just as easily and with the same technology. This makes the search for answers in classical calculus obsolete in many cases. This new paradigm comes at a cost: developing stable, convergent algorithms to evaluate functions is often more difficult than more classical analysis of these functions. For this reason, the subject is still being actively developed. However, it is possible to present many important ideas at an elementary level, as is done here.