Brian C. Hall - Quantum Theory for Mathematicians

Beginning in the late seventeenth century and continuing into the early eighteenth century, there was a vigorous debate in the scientific community over the nature of light. One camp, following the views of Isaac Newton, claimed that light consisted of a group of particles or corpuscles. The other camp, led by the Dutch physicist Christiaan Huygens, claimed that light was a wave. Newton argued that only a corpuscular theory could account for the observed tendency of light to travel in straight lines. Huygens and others, on the other hand, argued that a wave theory could explain numerous observed aspects of light, including the bending or refraction of light as it passes from one medium to another, as from air into water. Newtons reputation was such that his corpuscular theory remained the dominant one until the early nineteenth century.

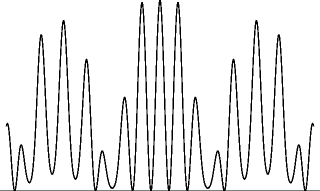
In 1804, Thomas Young published two papers describing and explaining his double-slit experiment. In this experiment, sunlight passes through a small hole in a piece of cardboard and strikes another piece of cardboard containing two small holes. The light then strikes a third piece of cardboard, where the pattern of light may be observed. Young observed fringes or alternating regions of high and low intensity for the light. Young believed that light was a wave and he postulated that these fringes were the result of interference between the waves emanating from the two holes. Young drew an analogy between light and water, where in the case of water, interference is readily observed. If two circular waves of water cross each other, there will be some points where a peak of one wave matches up with a trough of another wave, resulting in destructive interference , that is, a partial cancellation between the two waves, resulting in a small amplitude of the combined wave at that point. At other points, on the other hand, a peak in one wave will line up with a peak in the other, or a trough with a trough. At such points, there is constructive interference , with the result that the amplitude of the combined wave is large at that point. The pattern of constructive and destructive interference will produce something like a checkerboard pattern of alternating regions of large and small amplitudes in the combined wave. The dimensions of each region will be roughly on the order of the wavelength of the individual waves.

Based on this analogy with water waves, Young was able to explain the interference fringes that he observed and to predict the wavelength that light must have in order for the specific patterns he observed to occur. Based on his observations, Young claimed that the wavelength of visible light ranged from about 1/36,000 in. (about 700nm) at the red end of the spectrum to about 1/60,000 in. (about 425nm) at the violet end of the spectrum, results that agree with modern measurements.

Figure .

Despite the convincing nature of Youngs experiment, many proponents of the corpuscular theory of light remained unconvinced. In 1818, the French Academy of Sciences set up a competition for papers explaining the observed properties of light. One of the submissions was a paper by Augustin-Jean Fresnel in which he elaborated on Huygenss wave model of refraction. A supporter of the corpuscular theory of light, Simon-Denis Poisson read Fresnels submission and ridiculed it by pointing out that if that theory were true, light passing by an opaque disk would diffract around the edges of the disk to produce a bright spot in the center of the shadow of the disk, a prediction that Poisson considered absurd. Nevertheless, the head of the judging committee for the competition, Franois Arago, decided to put the issue to an experimental test and found that such a spot does in fact occur. Although this spot is often called Aragos spot, or even, ironically, Poissons spot, Arago eventually realized that the spot had been observed 100 years earlier in separate experiments by Delisle and Maraldi.

Aragos observation of Poissons spot led to widespread acceptance of the wave theory of light. This theory gained even greater acceptance in 1865, when James Clerk Maxwell put together what are today known as Maxwells equations. Maxwell showed that his equations predicted that electromagnetic waves would propagate at a certain speed, which agreed with the observed speed of light. Maxwell thus concluded that light is simply an electromagnetic wave. From 1865 until the end of the nineteenth century, the debate over the wave-versus-particle nature of light was considered to have been conclusively settled in favor of the wave theory.

In the early twentieth century, the wave theory of light began to experience new challenges. The first challenge came from the theory of blackbody radiation . In physics, a blackbody is an idealized object that perfectly absorbs all electromagnetic radiation that hits it. A blackbody can be approximated in the real world by an object with a highly absorbent surface such as lamp black. The problem of blackbody radiation concerns the distribution of electromagnetic radiation in a cavity within a blackbody. Although the walls of the blackbody absorb the radiation that hits it, thermal vibrations of the atoms making up the walls cause the blackbody to emit electromagnetic radiation. (At normal temperatures, most of the radiation emitted would be in the infrared range.)

In the cavity, then, electromagnetic radiation is constantly absorbed and re-emitted until thermal equilibrium is reached, at which point the absorption and emission of radiation are perfectly balanced at each frequency. According to the equipartition theorem of (classical) statistical mechanics, the energy in any given mode of electromagnetic radiation should be exponentially distributed, with an average value equal to k B T ,where T is the temperature and k B is Boltzmanns constant. (The temperature should be measured on a scale where absolute zero corresponds to T =0.) The difficulty with this prediction is that the average amount of energy is the same for every mode (hence the term equipartition). Thus, once one adds up over all modesof which there are infinitely manythe predicted amount of energy in the cavity is infinite. This strange prediction is referred to as the ultraviolet catastrophe , since the infinitude of the energy comes from the ultraviolet (high-frequency) end of the spectrum. This ultraviolet catastrophe does not seem to make physical sense and certainly does not match up with the observed energy spectrum within real-world blackbodies.