John Voight - Quaternion algebras

This book is an open access publication.

Quaternion algebras sit prominently at the intersection of many mathematical subjects. They capture essential features of noncommutative ring theory, number theory, 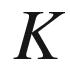-theory, group theory, geometric topology, Lie theory, functions of a complex variable, spectral theory of Riemannian manifolds, arithmetic geometry, representation theory, the Langlands programand the list goes on. Quaternion algebras are especially fruitful to study because they often reflect some of the general aspects of these subjects, while at the same time they remain amenable to concrete argumentation. Moreover, quaternions often encapsulate unique features that are absent from the general theory (even as they provide motivation for it).

With this in mind, the main goal in writing this text is to introduce a large subset of the above topics to graduate students interested in algebra, geometry, and number theory. To get the most out of reading this text, readers will likely want to have been exposed to some algebraic number theory, commutative algebra (e.g., module theory, localization, and tensor products), as well as the fundamentals of linear algebra, topology, and complex analysis. For certain sections, further experience with objects in differential geometry or arithmetic geometry (e.g., Riemannian manifolds and elliptic curves), may be useful. With these prerequisites in mind, I have endeavored to present the material in the simplest, motivated versionfull of rich interconnections and illustrative examplesso even if the reader is missing a piece of background, it can be quickly filled in.

Unfortunately, this text only scratches the surface of most of the topics covered in the book! In particular, some appearances of quaternion algebras in arithmetic geometry that are dear to me are absent, as they would substantially extend the length and scope of this already long book. I hope that the presentation herein will serve as a foundation upon which a detailed and more specialized treatment of these topics will be possible.

I have tried to maximize exposition of ideas and minimize technicality: sometimes I allow a quick and dirty proof, but sometimes the right level of generality (where things can be seen most clearly) is pretty abstract. So my efforts have resulted in a level of exposition that is occasionally uneven jumping between sections. I consider this a feature of the book, and I hope that the reader will agree and feel free to skip around (see How to use this book below). I tried to reboot at the beginning of each part and again at the beginning of each chapter, to refresh our motivation. For researchers working with quaternion algebras, I have tried to collect results otherwise scattered in the literature and to provide some clarifications, corrections, and complete proofs in the hope that this text will provide a convenient reference. In order to provide these features, to the extent possible I have opted for an organizational pattern that is horizontal rather than vertical: the text has many chapters, each representing a different slice of the theory.

I tried to compactify the text as much as possible, without sacrificing completeness. There were a few occasions when I thought a topic could use further elaboration or has evolved from the existing literature, but did not want to overburden the text; I collected these in a supplementary text