Valter Moretti - Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation
Here you can read online Valter Moretti - Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2018, publisher: Springer, genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation
- Author:
- Publisher:Springer
- Genre:
- Year:2018
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This book discusses the mathematical foundations of quantum theories. It offers an introductory text on linear functional analysis with a focus on Hilbert spaces, highlighting the spectral theory features that are relevant in physics. After exploring physical phenomenology, it then turns its attention to the formal and logical aspects of the theory.
Further, this Second Edition collects in one volume a number of useful rigorous results on the mathematical structure of quantum mechanics focusing in particular on von Neumann algebras, Superselection rules, the various notions of Quantum Symmetry and Symmetry Groups, and including a number of fundamental results on the algebraic formulation of quantum theories.
Intended for Masters and PhD students, both in physics and mathematics, the material is designed to be self-contained: it includes a summary of point-set topology and abstract measure theory, together with an appendix on differential geometry. The book also benefits established researchers by organizing and presenting the profusion of advanced material disseminated in the literature. Most chapters are accompanied by exercises, many of which are solved explicitly.
Valter Moretti: author's other books
Who wrote Spectral Theory and Quantum Mechanics: Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation? Find out the surname, the name of the author of the book and a list of all author's works by series.









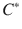 -algebras. Special attention is given to a series of results in spectral theory, such as the various formulations of the spectral theorem for bounded normal operators and not necessarily bounded, self-adjoint ones. This is, as a matter of fact, one further scope of the text. The mathematical formulation of Quantum Theories is confined to Chaps..
-algebras. Special attention is given to a series of results in spectral theory, such as the various formulations of the spectral theorem for bounded normal operators and not necessarily bounded, self-adjoint ones. This is, as a matter of fact, one further scope of the text. The mathematical formulation of Quantum Theories is confined to Chaps..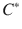 -algebras. Here one finds the proof of the GNS theorem and some consequences of purely mathematical flavour, like the general theorem of GelfandNajmark . This closing chapter also contains material on quantum symmetries in an algebraic setting. As an example the Weyl
-algebras. Here one finds the proof of the GNS theorem and some consequences of purely mathematical flavour, like the general theorem of GelfandNajmark . This closing chapter also contains material on quantum symmetries in an algebraic setting. As an example the Weyl