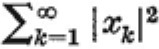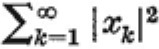Thomas F Jordan - Linear Operators for Quantum Mechanics

LINEAR OPERATORS FOR QUANTUM MECHANICS

THOMAS F. JORDAN

Physics Department

University of Minnesota, Duluth

DOVER PUBLICATIONS, INC.

Mineola, New York

Copyright

Copyright 1969, 1997 by Thomas F. Jordan

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2006, is an unabridged republication of the first edition published by John Wiley & Sons, Inc., New York, 1969.

Library of Congress Cataloging-in-Publication Data

Jordan, Thomas F., 1936

Linear operators for quantum mechanics / Thomas F. Jordan. p. cm.

Reprint. Originally published: New York : Wiley, 1968.

ISBN-13: 978-0-486-45329-3

ISBN-10: 0-486-45329-4 (pbk.)

1. Quantum theory. 2. Linear operators. I. Title.

QC174.5.J63 2007

530.1201'5157246dc22

2006048600

Manufactured in the United States by Courier Corporation

45329402

www.doverpublications.com

PREFACE

This is intended to be a companion to quantum-mechanics books. It treats the mathematics of linear operators used in quantum mechanics. Other elements of quantum mechanics are included only when they are needed for motivation or completeness. Different students may study the mathematical aspects at different times, depending on their backgrounds, interests, and needs. This is one reason for a separate treatment of the mathematics. I hope that in this compact presentation it will be easy for students of quantum mechanics to see the logic and simplicity of its mathematical structure.

My motivation to write this book has come from teaching first-year graduate quantum mechanics at the Universities of Rochester and Pittsburgh. The presentation is intended for a reader at that level. To round it out I have included topics not usually studied in the first year but which most students of quantum mechanics want to know sooner or later.

Originally quantum mechanics was atomic physics, but now it is also a basic language for solid-state, nuclear, and particle physics. The grammar of this language is the mathematics of linear operators. My philosophy is simply that knowing the grammar makes it easier to understand the language and easier to use it.

I take an entirely conventional view of the mathematical foundations of quantum mechanics. Most of it is in von Neumann's book. For equations of motion and representations of symmetry transformations I follow Wigner and Bargmann. The picture is filled in with recent work; for example, that of Jauch and co-workers.

My only serious deviation from standard physics practice is in diagonalizing operators. It seems to me that the difference between continuous and point spectra is important. I use projection operators on the ordinary Hilbert space, which naturally emphasizes this difference, instead of using vectors of infinite length to treat the continuous spectrum in analogy to the point spectrum. This just requires thinking about integrals with respect to dF(x) instead of f(x)dx.

The reader needs no technical knowledge of Lebesgue or Stieltjes integrals. An intuitive understanding of integration is sufficient.

I never give a proof just to establish that a statement is true. For that I have thought it sufficient to supply a reference. The proofs are intended to explain how or why statements are true and to provide exercises using some of the concepts or techniques. The references are not always intended to give credit for original work. They indicate where I think reading can continue with the most profit or least trouble.

Sections 20, 28, and 32 are not needed for the other sections that follow. It may be best to skip them the first time through. Section 11 also could be skipped.

THOMAS F. JORDAN

Pittsburgh, Pennsylvania

January 1968

ACKNOWLEDGMENTS

John R. Taylor responded very generously to my statement that I would appreciate criticism of the manuscript. He returned a thoroughly marked-up copy and spent many hours going over it with me to explain his ideas, in addition to writing letters about various points as he thought of them. This was immensely helpful to me as I worked through the manuscript again and led to significant improvements in every chapter. I am very grateful.

Leonard Parker made a detailed review of the manuscript at the request of the editor at John Wiley and Sons. His page-by-page and line-by-line criticism was an excellent guide for working through the manuscript. When I finished, I was so pleased to have had such a careful review that I asked to know the identity of the reviewer so that I could acknowledge his contribution to the book.

I want to thank Philip Stehle for much good advice about writing books in general and good criticism of this one in particular. I want to thank Johan de Swart, Gordon Fleming, Wolfgang Kundt, and Lochlainn O'Raifeartaigh for helpful comments, discussions, and criticism.

To Johan de Swart I am indebted also for a course of lectures that started my interest in the mathematics of linear operators some years ago.

Finally, I want to acknowledge my indebtedness to George Sudarshan who, first in teaching me to understand and appreciate the mathematical structure of quantum mechanics, and in discussing many of these topics, has contributed decisively to the concept and contents of this book and to my inspiration to write it.

T. F. J.

CONTENTS

LINEAR OPERATORS FOR QUANTUM MECHANICS

LINEAR SPACES AND LINEAR FUNCTIONALS

. VECTORS

The mathematical structures of quantum mechanics are built on linear spaces. To get the concept of a linear space we need only to generalize from vectors in ordinary three-dimensional position space to vectors in a space of arbitrary dimension. At the same time we consider vectors whose components in each direction are complex instead of real numbers. The algebraic properties of vectors, that they can be added and multiplied by numbers, are abstracted in the following.

Definitions. A linear space or vector space is a set of elements, called vectors, with an operation of addition, which for each pair of vectors and specifies a vector +, and an operation of scalar multiplication, which for each vector and number a specifies a vector a such that

for any vectors ,, and and numbers a and b. The numbers are called

Property (viii) justifies using the same symbol 0 for both the zero vector and the number zero. We use the notation for (1) and for + (1).

As examples of linear spaces consider the following:

(i) The set of all n-tuples of numbers with addition of two vectors = (x1, x2,... , xn) and = (y1, y2,... , yn) defined by += (x1 + y1x2+ y2,... , xn + yn) and multiplication of the vector by a scalar a defined by a = (ax1ax2,... , axn). We refer to this as n-dimensional Euclidean space.

(ii) The set of all infinite sequences of numbers (x1, x2,... , xk .. .) such that