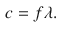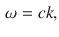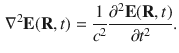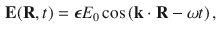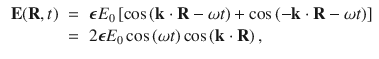As a science or engineering major, you are about to embark on what may be the most important course of your undergraduate career. Quantum mechanics is the foundation on which our current picture of the structure of matter is built. For students, an introductory course in quantum mechanics can be difficult and frustrating. When you studied Newtonian physics, it was easy to envision experiments involving the motion of particles moving under the influence of forces. Electromagnetism and optics were a bit more abstract once the concept of fields was introduced, but you are familiar with many optical effects such as colors of thin films, the rainbow, and diffraction from single or double slits. In quantum mechanics, it is more difficult conceptually to understand what is going on since you have very little day to day experience with the wave nature of matter. However, you can exploit your knowledge of both classical mechanics and optics to get a better feel for quantum mechanics.
I often begin a course in quantum mechanics asking students Why and when is quantum mechanics needed to explain the dynamics of a particle moving in a potential. In other words, when does a classical particle description fail? To understand and appreciate many aspects of quantum mechanics, you should always have this and a few other questions in the back of your mind. Question two might be How is the quantum mechanical solution of a given problem related to the corresponding problem in classical mechanics? Question three could be Is there a problem in optics with which I am familiar that can shed light on a given problem in quantum mechanics? You can add other questions to this list, but these are a good start.
Another key point in the study of quantum mechanics is not to lose track of the physics. There are many special functions, such as Hermite and Laguerre polynomials, that emerge from solutions of the Schrdinger equation, and the algebra can get a little complicated. As long as you remind yourself of the physical nature of the solution rather than the mathematical details, you will be in great shape. The reason for this is that most of the solutions share many common features. The specific form of the solutions may change, but the overall qualitative nature of the solutions is remarkably similar for many different problems. Moreover, with the availability of symbolic manipulation programs such as Mathematica, Maple, or Matlab, it is now easy to plot and evaluate any of these functions using a few keystrokes.
To help introduce the subject matter, I will present a very broad, qualitative overview of the way in which quantum mechanics was born, a birth that took about 2530 years. I will not worry about historical accuracy here, but simply try to give you a reasonable picture of the manner in which it became appreciated that a wave description of matter was needed in certain limits.
1.1 Electromagnetic Waves
Quantum mechanics is a wave theory. Since the wave properties of matter have many similarities to the wave properties of electromagnetic radiation, it wont hurt to review some of the fundamental properties of the electromagnetic field. The possible existence of electromagnetic waves followed from Maxwells equations. By combining the equations of electromagnetism, Maxwell arrived at a wave equation, in which the wave propagation speed in vacuum was equal to
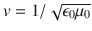
, where 0 is the permittivity and 0 the permeability of free space. Since these were known quantities in the nineteenth century, it was a simple matter to calculate v , which turned out to equal the speed of light. This result led Maxwell to conjecture that light was an electromagnetic phenomenon.
All electromagnetic waves travel in vacuum with speed c =2.99792458108 m/s, now defined as the speed of light. What distinguishes one type of electromagnetic wave from another is its wavelength or frequency f , which are related by
Instead of characterizing a wave by its frequency (which has units of cycles per second or Hz) and wavelength, we can equally well specify the angular frequency , =2 f , (which has units of radians per second or s 1) and the magnitude of the propagation vector (or wave vector ), defined by k =2/. With these definitions, Eq. () can be replaced by
which is known as a dispersion relation , relating frequency to wave vector. For electromagnetic radiation in vacuum the dispersion relation is linear.
The source of electromagnetic waves is oscillating or accelerating charges, which give rise to propagating electric and magnetic fields. The wave equation for the electric field vector E ( R , t ) at position R at time t in vacuum is
The simplest solution of this equation is also the most important, since it is a building block solution from which all other solutions can be constructed. The building block solution of the wave equation is the infinite, monochromatic, plane wave solution, having an electric field vector given by
where E 0 is the field amplitude and the polarization of the field is specified by a unit vector that is perpendicular to the propagation vector k of the field. There are two independent field polarizations possible for each propagation vector. The fact that k =0 follows from the requirement that E ( R , t ) =0 in vacuum. The field () corresponds to a wave that is infinite in extent and propagates in the k direction. Of course, no such wave exists in nature since it would uniformly fill all space.
As a consequence of the linearity of the wave equation, the sum of any two solutions of the wave equation is also a solution. This is known as a superposition principle . It is not difficult to visualize how waves add together. If, at the same time you are putting your finger in and out of water in a lake, someone else is also putting their finger in and out of the water, the resulting wave results from the actions of both your fingers. The important thing to remember is that it is the displacements or amplitudes of the waves that add, not their intensities. The intensity of a wave is proportional to the square of the wave amplitude.
For the time being, let us consider two waves having the same frequency and the same amplitude. If the two waves propagate in opposite directions, the total electric field vector is
a standing wave pattern. If you plot the wave amplitude at several different times as a function of position, you will find that there is an envelope for the wave that is fixed in spacethe wave stands there and oscillates within the envelope. The points of zero amplitude are called nodes of the field and the maxima (or minima) are called antinodes of the field. For a standing wave field in the x direction that is confined between two parallel mirrors separated by a distance L , the standing wave pattern will fit in for wavelengths equal to 2 L , L , 2 L /3, L /2, etc., as shown in Fig.. In this limit, the tangential component of the electric field vanishes at the mirrors, as required by the boundary conditions on the field. The condition















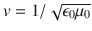 , where 0 is the permittivity and 0 the permeability of free space. Since these were known quantities in the nineteenth century, it was a simple matter to calculate v , which turned out to equal the speed of light. This result led Maxwell to conjecture that light was an electromagnetic phenomenon.
, where 0 is the permittivity and 0 the permeability of free space. Since these were known quantities in the nineteenth century, it was a simple matter to calculate v , which turned out to equal the speed of light. This result led Maxwell to conjecture that light was an electromagnetic phenomenon.