Dirac - Lectures on Quantum Mechanics

Paul A. M. Dirac

DOVER PUBLICATIONS, INC.
Mineola, New York

Bibliographical Note

This Dover edition, first published in 2001, is an unabridged reprint of the work originally published by the Belfer Graduate School of Science, Yeshiva University, New York, in 1964.

Library of Congress Cataloging-in-Publication Data

Dirac, P. A. M. (Paul Adrien Maurice), 1902

Lectures on quantum mechanics / by Paul A.M. Dirac.

p. cm.

Originally published: New York : Belfer Graduate School of Science, Yeshiva University, 1964.

ISBN-13: 978-0-486-41713-4 (pbk.)

ISBN-10: 0-486-41713-1 (pbk.)

1. Quantum theory. I. Title.

QC174.125 .D55 2001
530.12dc21

00-065608

Manufactured in the United States by Courier Corporation
41713109
www.doverpublications.com

DR. DIRAC

Im very happy to be here at Yeshiva and to have this chance to talk to you about some mathematical methods that I have been working on for a number of years. I would like first to describe in a few words the general object of these methods.

In atomic theory we have to deal with various fields. There are some fields which are very familiar, like the electromagnetic and the gravitational fields; but in recent times we have a number of other fields also to concern ourselves with, because according to the general ideas of De Broglie and Schrdinger every particle is associated with waves and these waves may be considered as a field. So we have in atomic physics the general problem of setting up a theory of various fields in interaction with each other. We need a theory conforming to the principles of quantum mechanics, but it is quite a difficult matter to get such a theory.

One can get a much simpler theory if one goes over to the corresponding classical mechanics, which is the form which quantum mechanics takes when one makes Plancks constant 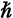tend to zero. It is very much easier to visualize what one is doing in terms of classical mechanics. It will be mainly about classical mechanics that I shall be talking in these lectures.

Now you may think that that is really not good enough, because classical mechanics is not good enough to describe Nature. Nature is described by quantum mechanics. Why should one, therefore, bother so much about classical mechanics? Well, the quantum field theories are, as I said, quite difficult and so far, people have been able to build up quantum field theories only for fairly simple kinds of fields with simple interactions between them. It is quite possible that these simple fields with the simple interactions between them are not adequate for a description of Nature. The successes which we get with quantum field theories are rather limited. One is continually running into difficulties and one would like to broaden ones basis and have some possibility of bringing more general fields into account. For example, one would like to take into account the possibility that Maxwells equations are not accurately valid. When one goes to distances very close to the charges that are producing the fields, one may have to modify Maxwells field theory so as to make it into a nonlinear electrodynamics. This is only one example of the kind of generalization which it is profitable to consider in our present state of ignorance of the basic ideas, the basic forces and the basic character of the fields of atomic theory.

In order to be able to start on this problem of dealing with more general fields, we must go over the classical theory. Now, if we can put the classical theory into the Hamiltonian form, then we can always apply certain standard rules so as to get a first approximation to a quantum theory. My talks will be mainly concerned with this problem of putting a general classical theory into the Hamiltonian form. When one has done that, one is well launched onto the path of getting an accurate quantum theory. One has, in any case, a first approximation.

Of course, this work is to be considered as a preliminary piece of work. The final conclusion of this piece of work must be to set up an accurate quantum theory, and that involves quite serious difficulties, difficulties of a fundamental character which people have been worrying over for quite a number of years. Some people are so much impressed by the difficulties of passing over from Hamiltonian classical mechanics to quantum mechanics that they think that maybe the whole method of working from Hamiltonian classical theory is a bad method. Particularly in the last few years people have been trying to set up alternative methods for getting quantum field theories. They have made quite considerable progress on these lines. They have obtained a number of conditions which have to be satisfied. Still I feel that these alternative methods, although they go quite a long way towards accounting for experimental results, will not lead to a final solution to the problem. I feel that there will always be something missing from them which we can only get by working from a Hamiltonian, or maybe from some generalization of the concept of a Hamiltonian. So I take the point of view that the Hamiltonian is really very important for quantum theory.

In fact, without using Hamiltonian methods one cannot solve some of the simplest problems in quantum theory, for example the problem of getting the Balmer formula for hydrogen, which was the very beginning of quantum mechanics. A Hamiltonian comes in therefore in very elementary ways and it seems to me that it is really quite essential to work from a Hamiltonian; so I want to talk to you about how far one can develop Hamiltonian methods.

I would like to begin in an elementary way and I take as my starting point an action principle. That is to say, I assume that there is an action integral which depends on the motion, such that, when one varies the motion, and puts down the conditions for the action integral to be stationary, one gets the equations of motion. The method of starting from an action principle has the one great advantage, that one can easily make the theory conform to the principle of relativity. We need our atomic theory to conform to relativity because in general we are dealing with particles moving with high velocities.

If we want to bring in the gravitational field, then we have to make our theory conform to the general principle of relativity, which means working with a space-time which is not flat. Now the gravitational field is not very important in atomic physics, because gravitational forces are extremely weak compared with the other kinds of forces which are present in atomic processes, and for practical purposes one can neglect the gravitational field. People have in recent years worked to some extent on bringing the gravitational field into the quantum theory, but I think that the main object of this work was the hope that bringing in the gravitational field might help to solve some of the difficulties. As far as one can see at present, that hope is not realized, and bringing in the gravitational field seems to add to the difficulties rather than remove them. So that there is not very much point at present in bringing gravitational fields into atomic theory. However, the methods which I am going to describe are powerful mathematical methods which would be available whether one brings in the gravitational field or not.

We start off with an action integral which I denote by

It is expressed as a time integral, the integrand