Contents
Pagebreaks of the print version

INTRODUCTION TO
QUANTUM MECHANICS
INTRODUCTION TO
QUANTUM MECHANICS
John Dirk Walecka College of William and Mary, USA
 Published by
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
Library of Congress Cataloging-in-Publication Data Names: Walecka, John Dirk, 1932 author. Title: Introduction to quantum mechanics / John Dirk Walecka, College of William and Mary, USA. Description: New Jersey : World Scientific Publishing Company, [2021] |
Includes bibliographical references and index.
Identifiers: LCCN 2021018728 (print) | LCCN 2021018729 (ebook) |
ISBN 9789811234729 (hardcover) | ISBN 9789811236112 (paperback) |
ISBN 9789811234736 (ebook) | ISBN 9789811234743 (mobi) Subjects: LCSH: Quantum theory. Classification: LCC QC174.12 .W345 2021 (print) | LCC QC174.12 (ebook) | DDC 530.12--dc23 LC record available at https://lccn.loc.gov/2021018728 LC ebook record available at https://lccn.loc.gov/2021018729 British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. Copyright 2021 by World Scientific Publishing Co. Pte. Ltd. All rights reserved.
This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. For any available supplementary material, please visit
https://www.worldscientific.com/worldscibooks/10.1142/12222#t=suppl Printed in Singapore For John and Ann
Preface
The author recently published a book entitled
Introduction to Electricity and Magnetism [Walecka-18]. It is based on an introductory course taught several years ago at Stanford, with over 400 students enrolled. The only requirements were an elementary knowledge of calculus and familiarity with vectors and Newtons laws; the development was otherwise self-contained. The lectures, although relatively concise, take one from Coulombs law to Maxwells equations and special relativity in a lucid and logical fashion.
Although never presented in an actual course, it occurred to the author that it would be fun to compose an equivalent set of lectures, aimed at the very best students, that would serve as a prequel to that Electricity and Magnetism text. This book has now also been published as Introduction to Classical Mechanics [Walecka-20]. The goal of this second text is to provide a clear and concise set of lectures that take one from the introduction and application of Newtons laws up to Hamiltons principle and the lagrangian mechanics of continuous systems. Both of these texts on classical physics are meant for initial one-quarter physics courses. These lectures, aimed at the very best students, assume a good concurrent course in calculus; they are otherwise self-contained. Both texts contain an extensive set of accessible problems that enhances and extends the coverage.
As an aid to teaching and learning, the solutions to these problems have now been published in additional texts [Walecka-19, Walecka-21]. The present text completes the first-year introduction to physics with a set of lectures on Introduction to Quantum Mechanics, the very successful theory of the microscopic world. The Schrdinger equation is motivated and presented. Several applications are explored, including scattering and transition rates. The applications are extended to include both quantum electrodynamics and quantum statistics. There is a discussion of quantum measurements.
The lectures then arrive at a formal presentation of quantum theory together with a summary of its postulates. A concluding chapter provides a brief introduction to relativistic quantum mechanics. An extensive set of accessible problems again enhances and extends the coverage. The goal of these three texts is to provide a good, understandable, oneyear introduction to the fundamentals of classical and quantum physics. It is my hope that students and teachers alike will find the use of these books rewarding and share some of the pleasure I took in writing them. Quantum mechanics is a huge field, and no attempt has been made to provide a complete bibliography.
The references given in the text are only directly relevant to the discussion at hand. It is important, however, to mention some of the good, existing books that the author has found particularly useful, such as [Wentzel (1949); Bjorken and Drell (1964); Bjorken and Drell (1965); Schiff (1968); Itzykson and Zuber (1980); Landau and Lifshitz (1981); Shankar (1994); Merzbacher (1997); Gottfried and Yan (2004); Feynman and Hibbs (2010)]. In addition, appendix B lists some significant names in quantum mechanics, both in its theory and in its applications. I would like to once again thank my editor, Ms. Lakshmi Narayanan, for her help and support on this project. Williamsburg, Virginia
January 8, 2021 John Dirk Walecka
Governors Distinguished CEBAF
Professor of Physics, emeritus
College of William and Mary
Contents
Chapter 1
Motivation
1.1 Classical Optics
Consider a non-dispersive wave which is the real part of
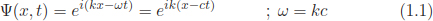
Here
c is the velocity of the wave, and the frequency and wavelength are related by

As we have seen, this could be an electromagnetic wave in vacuum, a transverse wave on a string under tension, or the sound wave in a medium.
Williamsburg, Virginia
January 8, 2021 John Dirk Walecka
Governors Distinguished CEBAF
Professor of Physics, emeritus
College of William and MaryContents
Chapter 1
Motivation
1.1 Classical Optics
Consider a non-dispersive wave which is the real part of
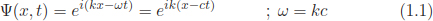
Here
c is the velocity of the wave, and the frequency and wavelength are related by

As we have seen, this could be an electromagnetic wave in vacuum, a transverse wave on a string under tension, or the sound wave in a medium.
This wave satisfies the wave equation 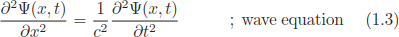 We have also seen that a linear combination of two such waves with slightly different wavenumbers
We have also seen that a linear combination of two such waves with slightly different wavenumbers












 Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Names: Walecka, John Dirk, 1932 author. Title: Introduction to quantum mechanics / John Dirk Walecka, College of William and Mary, USA. Description: New Jersey : World Scientific Publishing Company, [2021] |
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Names: Walecka, John Dirk, 1932 author. Title: Introduction to quantum mechanics / John Dirk Walecka, College of William and Mary, USA. Description: New Jersey : World Scientific Publishing Company, [2021] |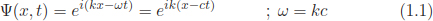 Here c is the velocity of the wave, and the frequency and wavelength are related by
Here c is the velocity of the wave, and the frequency and wavelength are related by  As we have seen, this could be an electromagnetic wave in vacuum, a transverse wave on a string under tension, or the sound wave in a medium. Williamsburg, Virginia
As we have seen, this could be an electromagnetic wave in vacuum, a transverse wave on a string under tension, or the sound wave in a medium. Williamsburg, Virginia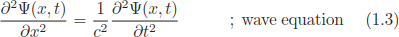 We have also seen that a linear combination of two such waves with slightly different wavenumbers
We have also seen that a linear combination of two such waves with slightly different wavenumbers