David Morin - Introduction to Classical Mechanics with Problems and Solutions

This textbook covers all the standard introductory topics in classical mechanics, including Newtons laws, oscillations, energy, momentum, angular momentum, planetary motion, and special relativity. It also explores more advanced topics, such as normal modes, the Lagrangian method, gyroscopic motion, fictitious forces, 4-vectors, and general relativity.

It contains more than 250 problems with detailed solutions so students can easily check their understanding of the topic. There are also over 350 unworked exercises, which are ideal for homework assignments. Password-protected solutions are available to instructors at www.cambridge.org/9780521876223. The vast number of problems alone makes it an ideal supplementary book for all levels of undergraduate physics courses in classical mechanics. The text also includes many additional remarks which discuss issues that are often glossed over in other textbooks, and it is thoroughly illustrated with more than 600 figures to help demonstrate key concepts.

D AVID M ORIN is a Lecturer in the Physics Department at Harvard University. He received his Ph.D. in theoretical particle physics from Harvard in 1996. When not writing physics limericks or thinking of new problems whose answers involve e or the golden ratio, he can be found running along the Charles River or hiking in the White Mountains of New Hampshire.

With Problems and Solutions

David Morin

Harvard University

CAMBRIDGE UNIVERSITY PRESS
Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, So Paulo,
Delhi, Tokyo, Mexico City

Cambridge University Press
The Edinburgh Building, Cambridge CB2 8RU, UK

Published in the United States of America by Cambridge University Press, New York

www.cambridge.org
Information on this title: www.cambridge.org/9780521876223

D. Morin 2007

This publication is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press.

First published 2008
7th printing 2012

Printed in the United Kingdom at the University Press, Cambridge

A catalogue record for this publication is available from the British Library

ISBN 978-0-521-87622-3 Hardback

Cambridge University Press has no responsibility for the persistence or accuracy of URLs for external or third party internet websites referred to in this publication, and does not guarantee that any content on such websites is, and will remain accurate or appropriate.

To Allen Gerry and Neil Tame,
who took the time
to give a group of kids
some really cool problems

There once was a classical theory,
Of which quantum disciples were leery.
They said, Why spend so long
On a theory thats wrong?
Well, it works for your everyday query!

Damped harmonic motion

Angular momentum, Part I (Constant )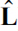

Problems

This book grew out of Harvard Universitys honors freshman mechanics course. It is essentially two books in one. Roughly half of each chapter follows the form of a normal textbook, consisting of text, along with exercises suitable for homework assignments. The other half takes the form of a problem book, with all sorts of problems (and solutions) of varying degrees of difficulty. Ive always thought that doing problems is the best way to learn, so if youve been searching for a supply to puzzle over, I think this will keep you busy for a while.

This book is somewhat of a quirky one, so let me say right at the start how I imagine it being used:

• As the primary text for honors freshman mechanics courses. My original motivation for writing it was the fact that there didnt exist a suitable book for Harvards freshman course. So after nine years of using updated versions in the class, here is the finished product.
• As a supplementary text for standard freshman courses for physics majors. Although this book starts at the beginning of mechanics and is self contained, it doesnt spend as much time on the introductory material as other freshman books do. I therefore dont recommend using this as the only text for a standard freshman mechanics course. However, it will make an extremely useful supplement, both as a problem book for all students, and as a more advanced textbook for students who want to dive further into certain topics.
• As a supplementary text for upper-level mechanics courses, or as the primary text which is supplemented with another book for additional topics often covered in upper-level courses, such as Hamiltons equations, fluids, chaos, Fourier analysis, electricity and magnetism applications, etc. With all of the worked examples and in-depth discussions, you really cant go wrong in pairing up this book with another one.
• As a problem book for anyone who likes solving physics problems. This audience ranges from advanced high-school students, who I think will have a ball with it, to undergraduate and graduate students who want some amusing problems to ponder, to professors who are looking for a new supply of problems to use in their classes, and finally to anyone with a desire to learn about physics by doing problems. If you want, you can consider this to be a problem book that also happens to have comprehensive introductions to each topics set of problems. With about 250 problems (with included solutions) and 350 exercises (without included solutions), in addition to all the examples in the text, I think youll get your moneys worth! But just in case, I threw in 600 figures, 50 limericks, nine appearances of the golden ratio, and one cameo of e.

The prerequisites for the book are solid high-school foundations in mechanics (no electricity and magnetism required) and single-variable calculus. There are two minor exceptions to this. First, a few sections rely on multivariable calculus, so I have given a review of this in ) rely on matrices and other elementary topics from linear algebra. But a basic understanding of matrices should suffice here.

A brief outline of the book is as follows. deals with conservation of energy and momentum. Youve probably seen much of this before, but it has lots of neat problems.

In , we introduce the Lagrangian method, which will most likely be new to you. It looks rather formidable at first, but its really not all that rough. There are difficult concepts at the heart of the subject, but the nice thing is that the technique is easy to apply. The situation here is analogous to taking a derivative in calculus; there are substantive concepts on which the theory rests, but the act of taking a derivative is fairly straightforward.

deals with accelerating reference frames and fictitious forces.

covers a few topics from General Relativity. Its impossible for one chapter to do this subject justice, of course, so well just look at some basic (but still very interesting) examples. Finally, the appendices cover various useful, but slightly tangential, topics.

Throughout the book, I have included many Remarks. These are written in a slightly smaller font than the surrounding text. They begin with a small-capital R EMARK and end with a shamrock (). The purpose of these remarks is to say something that needs to be said, without disrupting the overall flow of the argument. In some sense these are extra thoughts, although they are invariably useful in understanding what is going on. They are usually more informal than the rest of the text, and I reserve the right to use them to occasionally babble about things that I find interesting, but that you may find tangential. For the most part, however, the remarks address issues that arise naturally in the course of the discussion. I often make use of Remarks at the ends of the solutions to problems, where the obvious thing to do is to check limiting cases (this topic is discussed in ). However, in this case, the remarks are