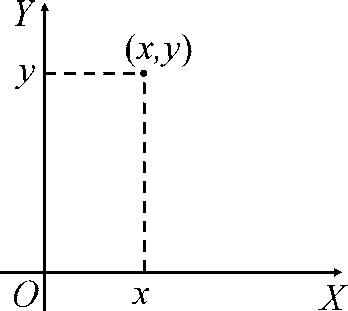Hiqmet Kamberaj - Classical Mechanics

Often in physics, as we will see, we deal with the location in space, which is done with the use of coordinates. The ones most often used are the Cartesian coordinates, (x,y) . These are used in a Cartesian coordinate system, where the horizontal and vertical axes intersect at a single point, called the origin (see also ). Cartesian coordinates are also called rectangular coordinates.

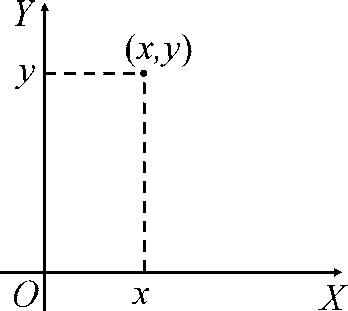
Figure 1.1 Points in a Cartesian coordinate system labeled with coordinates (x,y) .

For convenience reasons sometimes we represent a point in a plane by its plane polar coordinates (r,) , shown in . In the polar coordinate system, r is the distance from the origin to the point having Cartesian coordinates (x,y) , and is the angle between r- and x-axis, taken as the positive x-axis. The angle is usually measured counterclockwise from the positive x-axis.

From the right triangle in , we can obtain the Cartesian coordinates as a function of the plane polar coordinates of any point using the following equations:

Using the trigonometric relations, tan=sin/cos and sin2+cos2=1 , we can find that

Equation () can be used to relate the Cartesian coordinated (x,y) with the polar coordinates (r,) only when is defined as in , with positive angle measured counterclockwise from the positive x-axis.

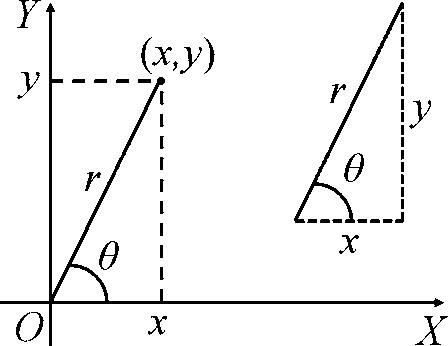
Figure 1.2 (a) The plane polar coordinates of a point are represented by the distance r and the angle , where is measured counterclockwise from the positive x-axis. (b) The right triangle used to relate (x,y) to (r,) .

These standard conventions are often used from some scientific calculators to perform conversions between Cartesian and polar coordinates. Moreover, if we choose the reference axis for the polar angle to be different from the positive x-axis or if the sense of increasing is different, then the expressions in eq.() will change.

In physics, there exist both scalar quantities and vector quantities. For example, for expressing the temperature, we need its value (that is a number) and the units, either in degrees Celsius ( C ) or degrees Fahrenheit ( F ). Therefore, we say that temperature is a scalar quantity, entirely defined by a number and appropriate units. Other scalar quantities include volume, mass, and time intervals.

Definition 1.1 (Scalar quantity).

By definition, a scalar quantity is specified by a single value with an appropriate unit. A scalar quantity has no direction.

The scalar quantities obey the same rules of ordinary arithmetic when used for calculations.

Often, when we determine an objects position (say a car) that starts the motion from some reference frames origin, it is necessary to know both its speed and its direction. Both the speed and the direction are named as a single quantity, velocity. Therefore, velocity is a vector quantity because it depends on the direction. As we will see, it is defined as a physical quantity that is completely specified by a value (speed) with appropriate units and direction.

Definition 1.2 (Vector quantity).

By definition, a vector quantity is determined by both magnitude and direction.

The displacement is another example of the vector quantity. Suppose a particle moves from point A to point B along a straight path, as shown in , its displacement is still the arrow drawn from A to B.

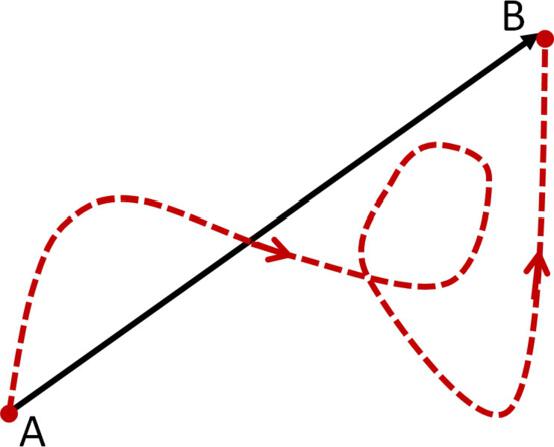
Figure 1.3 The trajectory of a particle moving from some point A to some point B.

Here, we will use a boldface letter (A) to represent a vector quantity. Besides, the vector can be notated with an arrow over a letter. The magnitude of the vector A will be written either A or |A| . The magnitude of a vector also has physical units; for example, the displacement has SI units of meters and the velocity meters per second.

1.3 Some properties of vectors

1.3.1 Equality of two vectors

Definition 1.3 (Equal vectors).

Two vectors A and B may be defined to be equal if they have the same magnitude and the same direction. That is, A=B only if A=B and if A and B point in the same direction along parallel lines.

In we show several equal vectors parallel to each other even though they all have different starting points. Using this property in a diagram, we can move a vector to a position parallel to itself without affecting the vector. That is often used to draw the free diagram of forces.

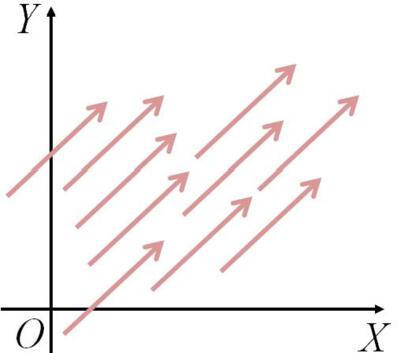
Figure 1.4 Illustration of equal vectors.

1.3.2 Adding vectors

Triangle rule of addition

To add vector B to vector A, we will use the geometric description. That is, first, draw vector A, with its magnitude represented by a convenient scale, on graph paper and then draw vector B to the same scale with its tail starting from the tip of A, as shown in .

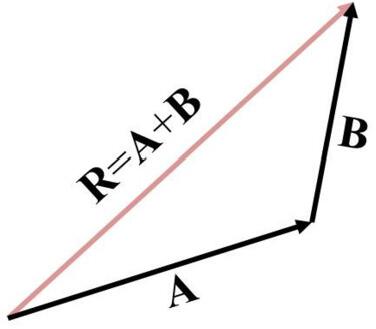
Figure 1.5 The sum of two vectors A and B is the vector R=A+B .

The final resultant vector R is written as

(1.3) R=A+B.

R is the vector drawn from the tail of A to the tip of B. This procedure is known as the triangle rule of addition.

We can use the same geometrical description to add more than two vectors, as shown in , for the case of four different vectors. The resultant vector R is the vector drawn from the tail of the first vector to the tip of the last vector completing in this way a polygon:

(1.4) R=A+B+C+D.

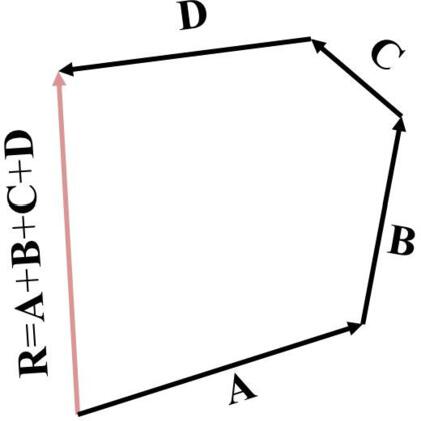
Figure 1.6 The sum of four vectors, namely A, B, C and D, is the vector R=A+B+C+D .

Parallelogram rule of addition