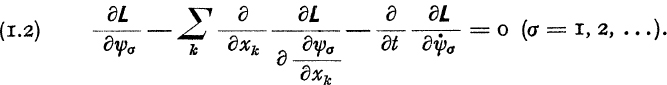QUANTUM THEORY
OF FIELDS
Gregor Wentzel
Translated by Charlotte Houtermans
and J. M. Jauch DOVER PUBLICATIONS, INC.
Mineola, New York
Bibliographical Note This Dover edition, first published in 2003, is an unabridged republication of the work originally published in 1949 by Interscience Publishers, Inc., New York. This is an English translation of the work titled
Einfhrung in die Quantentheorie der Wellenfelder, published in 1942 by Franz Deuticke, Vienna.
Library of Congress Cataloging-in-Publication Data Wentzel, Gregor, 1898 [Einfhrung in die Quantentheorie der Wellenfelder. Jauch. p. cm. cm.
Originally published: New York : Interscience Publishers, 1949. Includes index. eISBN-13: 978-0-486-17449-5 ISBN 0-486-43245-9 (pbk.) 1. Quantum theory. I. Title.
QC174.12.W4613 2003 530.12dc22 2003055498 Manufactured in the United States of America Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501
Preface
In research in theoretical physics of the past years, work in the quantum theory of fields has held a significant place. The student who wishes to become acquainted, by means of periodicals, with this branch of study will often find access difficult, even though he may be fully conversant with elementary quantum mechanics. Many of my colleagues who have introduced their pupils to the original literature agree with me in this. This book may help make that access easier. Naturally, I have wondered whether the theory is well enough established to be dealt with in a text-book, but I believe I can ignore such considerations.
Certainly the theory has a problematic aspect (see Self-energy in the index). If, in the near future, important progress in this theory could be foreseen, we might expect some parts of this book to become rapidly obsolete, yet we can hardly hope for so favorable a development at the present time. While waiting for the liberating new ideas, we must depend on our present theory, and so it seems worth while to make the theory more easily accessible to the interested. Only those who know the theory can understand the problems. As the title suggests, this book is only an introduction, not an all-inclusive account. The didactic purpose precludes a too systematic approach.
It appeared appropriate to start with the canonical quantization rules of elementary quantum mechanics (Heisenbergs commutation relations), even though further investigation shows that these rules are too narrow and must be generalized, as, for example, in dealing with particles obeying the Pauli exclusion principle. On the other hand, I have not attempted to deal separately and in detail with the classical theory of wave fields. No doubt, it would have been instructive to illustrate certain deductions in quantum theory by pointing out the corresponding classical considerations; however, since the operator technique of quantum mechanics often simplifies the calculations, I have preferably used the quantum version. In the first chapter the fundamentals of the theory are dealt with in a general manner, that is, without specification of the field equations or the Lagrange function. The remaining chapters are devoted to particular field types which by means of quantization are associated with particles of various spin, charge, ) as illustrations. The sections in small type are devoted to special questions and applications.
The reader may omit these if he wishes. It is assumed that the reader is acquainted with such fundamentals as are to be found in the current text-book literature. This applies not only to elementary quantum mechanics but especially to Diracs wave mechanics of spin-electrons (from on). The reader will find the necessary preparation for instance in the article by W. Pauli in Geiger-Scheels Handbuch der Physik, Volume 24, I. Zurich G.
WENTZEL August, 1942
Preface to the English Edition
I hope the reader will welcome the English translation of my bookinitiated by Interscience Publishersas much as I do. A rough translation of the text was made by Mrs. Charlotte Houtermans, and then revised and corrected scientifically and linguistically by Dr. J. M. Dr. F. F.
Coester was kind enough to read proof of the galleys and to prepare the index. The demand for an introduction into the quantum theory of fields seems to be even larger today than some years ago when this book was written. New interest in the subject has been awakened by recent experimental discoveries: the fine structure anomalies of the hydrogen levels, and the correction to the magnetic moment of the electron, which have been interpreted as electromagnetic self-energy terms; the observation of several kinds of mesons and their artificial production, marking a new development that promises a much better understanding of mesons and may eventually lead to an improved meson field theory of nuclear interactions. As to quantum electrodynamics, it was not possible to incorporate any references to the new theoretical developments into the present edition. We must be content to provide the reader with such basic information as will enable him to follow independently the original literature now appearing in the periodicals. In the chapters on meson theory no changes were necessary except in , dealing with the applications to problems of nuclear physics; here it was easy to modernize the text and to adapt it to the present state of knowledge.
In various sections throughout the book references to more recent publications have been added. The most significant addition to the original is the Appendix, on the general construction of the energy-momentum tensor according to F. J. Belinfante. I hope that the book proves useful to many readers in the English-speaking world. University of Chicago G.
WENTZEL January, 1949 QUANTUM THEORY
OF FIELDS
Chapter I
General Principles
1. The Canonical Formalism
In classical physics a field is described by one or several (real) space-time functions (
x,
t) which satisfy certain partial differential equations, the so- called field equations. An alternative procedure is to start with a variational principle chosen in such a way that its Euler differential equations are the same field equations. Let
L be a function of the (
x,
t) and of their first time and space derivatives:

By integration over a volume
V and a time interval from
t to
t we form:
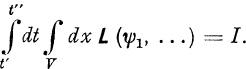
Varying the function for a fixed region of integration:
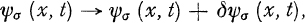
subject to the restriction that the variations vanish at the boundary of the domain of integration (i. e., at the surface of the volume
V and for
t =
t and
t =
t), one obtains in the familiar way:
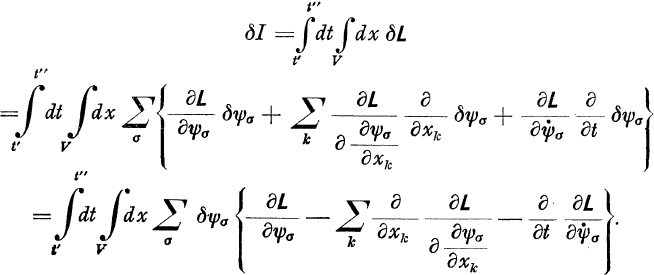
We require now that the classical field be determined by the condition that the integral
I shall be stationary (
I = o) for arbitrary variations which satisfy the above-mentioned conditions and for an arbitrary choice of the integration region. From this it follows that for all times and for all positions:
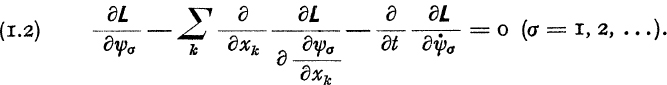











 By integration over a volume V and a time interval from t to t we form:
By integration over a volume V and a time interval from t to t we form: 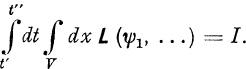 Varying the function for a fixed region of integration:
Varying the function for a fixed region of integration: 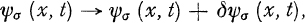 subject to the restriction that the variations vanish at the boundary of the domain of integration (i. e., at the surface of the volume V and for t = t and t = t), one obtains in the familiar way:
subject to the restriction that the variations vanish at the boundary of the domain of integration (i. e., at the surface of the volume V and for t = t and t = t), one obtains in the familiar way: 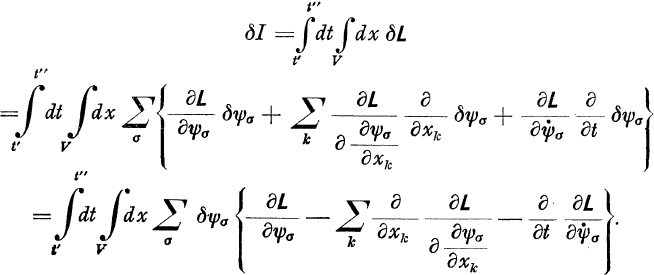 We require now that the classical field be determined by the condition that the integral I shall be stationary ( I = o) for arbitrary variations which satisfy the above-mentioned conditions and for an arbitrary choice of the integration region. From this it follows that for all times and for all positions:
We require now that the classical field be determined by the condition that the integral I shall be stationary ( I = o) for arbitrary variations which satisfy the above-mentioned conditions and for an arbitrary choice of the integration region. From this it follows that for all times and for all positions: