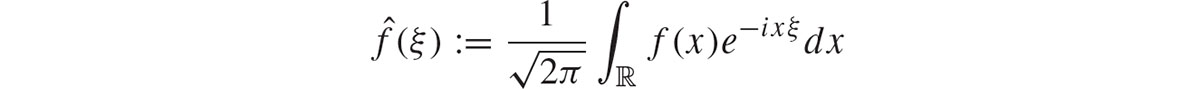A Mathematical
Companion to
Quantum Mechanics Copyright
Copyright Copyright 2019 by Shlomo Sternberg All rights reserved.
Bibliographical NoteA Mathematical Companion to Quantum Mechanics is a new work, first published by Dover Publications, Inc., in 2019.
Library of Congress Cataloging-in-Publication Data Names: Sternberg, Shlomo, author. Title: A mathematical companion to quantum mechanics / Shlomo Sternberg (professor of mathematics emeritus, Harvard University). Description: Mineola, New York : Dover Publications, Inc., 2019. | Mathematical physics. | Mathematical physics.
Classification: LCC QC174.12 .S8445 2019 | DDC 530.12dc23 LC record available at https://lccn.loc.gov/2018044258 Manufactured in the United States by LSC Communications 82689901 2019 www.doverpublications.com ToAviva GreenTable of ContentsA Mathematical
Companion to
Quantum MechanicsChapter 1Introduction Over the years, I taught Theory of Functions of a Real Variable at Harvard many times. In addition to standard material such as functional analysis, measure, and integration theory, I included elementary mathematics for quantum mechanics. I thought it would be useful to extract this material and gather it together. There are many books on this subject. The closest competitor is the excellent book Mathematical Methods in Quantum Mechanics by Teschl [], but my approach to many topics is sufficiently different to warrant the effort of organizing this book. Of course, the multivolume book by Reed and Simon [] is the classic text on the subject, which goes far beyond anything I cover, and is absolutely necessary for any serious student.
I dont deal with the philosophical and mathematical foundations of quantum mechanics for which I refer to Mackeys classic []. This book presents mathematical methods. As this book is assembled from many lectures, it is not in linear order. It should be regarded as a potpourri of various topics. Nevertheless, here is a rough outline: A key ingredient is the spectral theorem for self-adjoint operators. For example, the first proof for possibly unbounded self-adjoint operators occurs in Wintners book of 1929 [.
I know at least eight different proofs of this theorem. I derive the spectral theorem from the Fourier inversion formula, which says that (for nice functions) f, 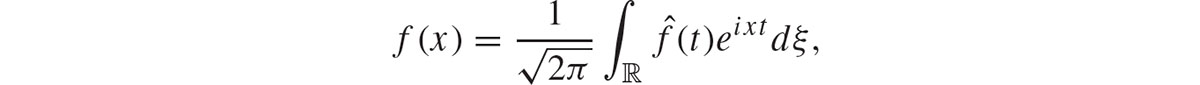 where
where 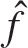 denotes the Fourier transform of f. If we replace x by A and write U (t) instead of eitA, this suggests that we define
denotes the Fourier transform of f. If we replace x by A and write U (t) instead of eitA, this suggests that we define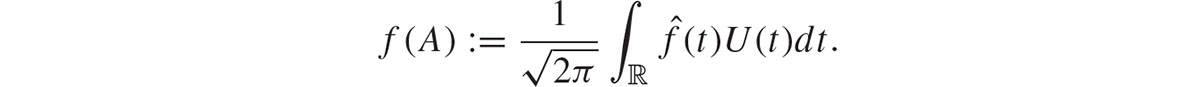 This defines a functional calculus
This defines a functional calculus 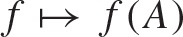 which has nice properties, as we check in . The next big ticket item is Weyls 1909 theorem [ involves more discussion on the details of Weyls theorem. One important consequence is to a Schrdinger operator of the form H = H0 + V, where H0 is the free Hamiltonian and V is a potential. Weyls theorem implies that if V (x) as x then there is no essential spectrum so the spectrum of H consists entirely of eigenvalues of finite multiplicity, while if V (x) 0 as x then the essential spectrum of H is the same as that of H0.
which has nice properties, as we check in . The next big ticket item is Weyls 1909 theorem [ involves more discussion on the details of Weyls theorem. One important consequence is to a Schrdinger operator of the form H = H0 + V, where H0 is the free Hamiltonian and V is a potential. Weyls theorem implies that if V (x) as x then there is no essential spectrum so the spectrum of H consists entirely of eigenvalues of finite multiplicity, while if V (x) 0 as x then the essential spectrum of H is the same as that of H0.
In to get the needed extension. In , I present Wintners proof, which gives the functional calculus directly for bounded Borel functions. I did not do the Wintner approach from the start because it depends on the Borel transformand the Stieltjes inversion formula, which are not as well known (or as standard) as the Fourier transform and its inversion formula. is devoted to the L2 version of the spectral theorem, which says that any self-adjoint operator is unitarily equivalent to multiplication by a real function on a measure space. In contrast to the functional calculus versions, this isomorphism is highly non-canonical, but it allows us to discuss fractional powers of a non-negative self-adjoint operator. are devoted to quantum mechanics in one dimension, with some results going back to the work of Sturm circa 1850. does some three-dimensional computations. is devoted to Ruelles theorem: It is a truism in atomic physics or quantum chemistry courses that the eigenstates of the Schrdinger operator for atomic electrons are the bound statesthe ones that remain bound to the nucleusand that the scattering states which fly off in large positive or negative times correspond to the continuous spectrum. is devoted to Ruelles theorem: It is a truism in atomic physics or quantum chemistry courses that the eigenstates of the Schrdinger operator for atomic electrons are the bound statesthe ones that remain bound to the nucleusand that the scattering states which fly off in large positive or negative times correspond to the continuous spectrum.
Ruelles theorem gives a mathematical justification for this truism. At the other extreme, Agmons theorem says that under appropriate conditions the eigenvectors (which correspond to bound states) die off exponentially at infinity. gives a watered down version of Agmons theorem. In I return once more to the spectral theorem, this time giving Lorchs proof which makes use of a beautifully complex variable style calculus due Riesz and Dunford. give a smattering of quantum mechanical scattering theory, including a chapter on Hughens principle of wave mechanics. returns to the subject of semigroups and presents an important theorem of Chernoff and some of its consequences. gives some background material. gives some background material.
The first two chapters of [ several times. I use the Cauchy integral formula and Cauchys theorem (which can be found near the opening of any text on complex variable theory) throughout the book. I thank Chen He and Rob Lowry for proofreading the text. Chapter 2The Fourier Transform I will start with standard facts about the Fourier transform from which I will derive the spectral theorem for bounded self-adjoint operators in . 2.0.1Conventions The space S consists of all complex valued functions on that are infinitely differentiable and vanish at infinity rapidly with all their derivatives in the sense that 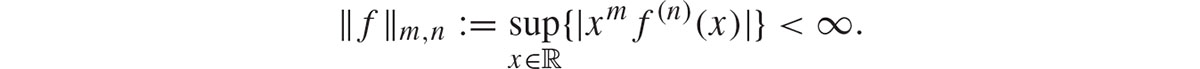 The m,n give a family of semi-norms on S making S into a Frchet spacethat is, a vector space whose topology is determined by a countable family of semi-norms. We use the measure
The m,n give a family of semi-norms on S making S into a Frchet spacethat is, a vector space whose topology is determined by a countable family of semi-norms. We use the measure 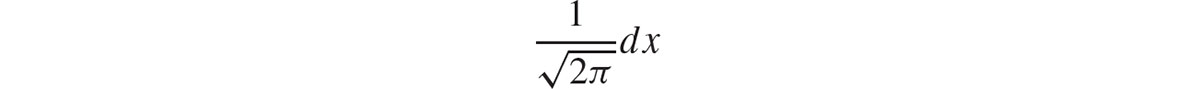 on and so define the Fourier transform of an element of S by
on and so define the Fourier transform of an element of S by 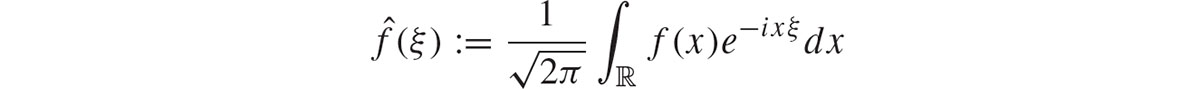














 Copyright Copyright 2019 by Shlomo Sternberg All rights reserved. Bibliographical NoteA Mathematical Companion to Quantum Mechanics is a new work, first published by Dover Publications, Inc., in 2019. Library of Congress Cataloging-in-Publication Data Names: Sternberg, Shlomo, author. Title: A mathematical companion to quantum mechanics / Shlomo Sternberg (professor of mathematics emeritus, Harvard University). Description: Mineola, New York : Dover Publications, Inc., 2019. | Mathematical physics. | Mathematical physics.
Copyright Copyright 2019 by Shlomo Sternberg All rights reserved. Bibliographical NoteA Mathematical Companion to Quantum Mechanics is a new work, first published by Dover Publications, Inc., in 2019. Library of Congress Cataloging-in-Publication Data Names: Sternberg, Shlomo, author. Title: A mathematical companion to quantum mechanics / Shlomo Sternberg (professor of mathematics emeritus, Harvard University). Description: Mineola, New York : Dover Publications, Inc., 2019. | Mathematical physics. | Mathematical physics. 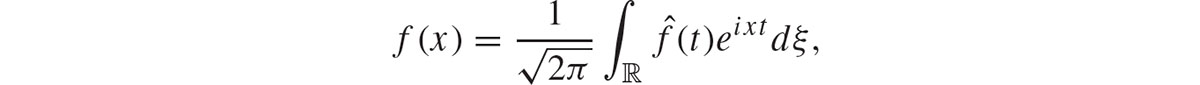 where
where 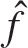 denotes the Fourier transform of f. If we replace x by A and write U (t) instead of eitA, this suggests that we define
denotes the Fourier transform of f. If we replace x by A and write U (t) instead of eitA, this suggests that we define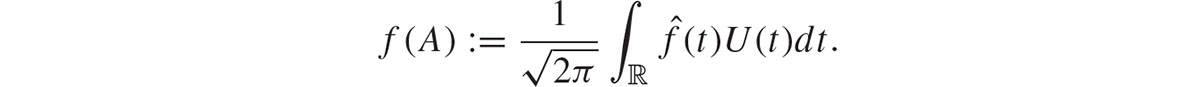 This defines a functional calculus
This defines a functional calculus 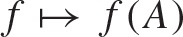 which has nice properties, as we check in . The next big ticket item is Weyls 1909 theorem [ involves more discussion on the details of Weyls theorem. One important consequence is to a Schrdinger operator of the form H = H0 + V, where H0 is the free Hamiltonian and V is a potential. Weyls theorem implies that if V (x) as x then there is no essential spectrum so the spectrum of H consists entirely of eigenvalues of finite multiplicity, while if V (x) 0 as x then the essential spectrum of H is the same as that of H0.
which has nice properties, as we check in . The next big ticket item is Weyls 1909 theorem [ involves more discussion on the details of Weyls theorem. One important consequence is to a Schrdinger operator of the form H = H0 + V, where H0 is the free Hamiltonian and V is a potential. Weyls theorem implies that if V (x) as x then there is no essential spectrum so the spectrum of H consists entirely of eigenvalues of finite multiplicity, while if V (x) 0 as x then the essential spectrum of H is the same as that of H0.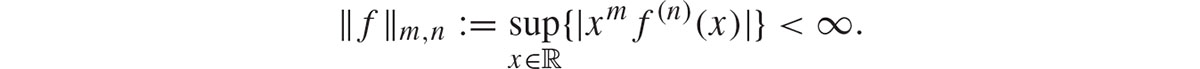 The m,n give a family of semi-norms on S making S into a Frchet spacethat is, a vector space whose topology is determined by a countable family of semi-norms. We use the measure
The m,n give a family of semi-norms on S making S into a Frchet spacethat is, a vector space whose topology is determined by a countable family of semi-norms. We use the measure 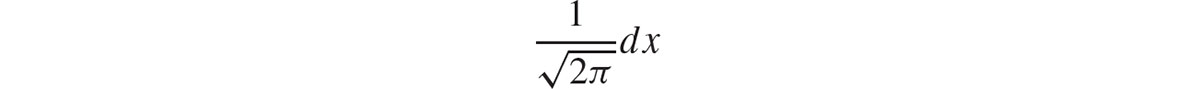 on and so define the Fourier transform of an element of S by
on and so define the Fourier transform of an element of S by