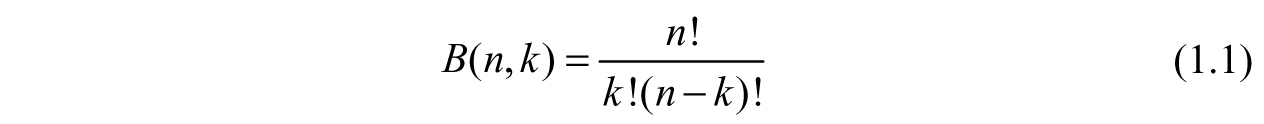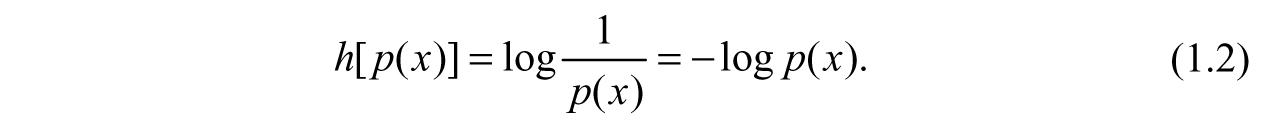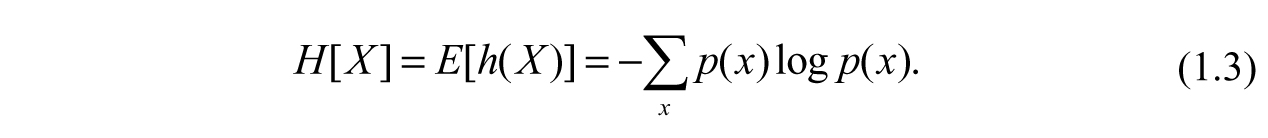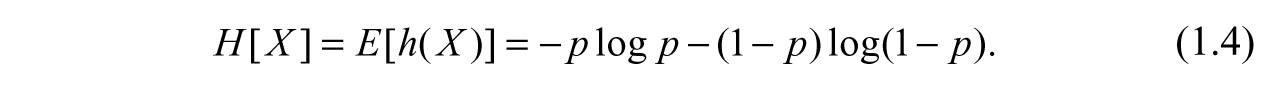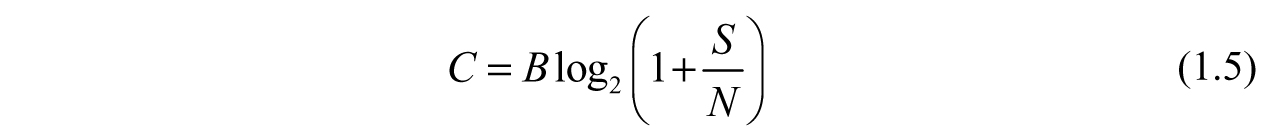AN INTRODUCTION TO QUANTUM COMMUNICATION
AN INTRODUCTION TO QUANTUM COMMUNICATION
VINOD K. MISHRA

An Introduction to Quantum Communication
Copyright Momentum Press, LLC, 2016.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any meanselectronic, mechanical, photocopy, recording, or any otherexcept for brief quotations, not to exceed 250 words, without the prior permission of the publisher.
First published in 2016 by
Momentum Press, LLC
222 East 46th Street, New York, NY 10017
www.momentumpress.net
ISBN-13:978-1-60650-556-4 (print)
ISBN-13:978-1-60650-557-1 (e-book)
Momentum Press Communications and Signal Processing Collection
Cover and interior design by S4Carlisle Publishing Service Private Ltd.
Chennai, India
10 9 8 7 6 5 4 3 2 1
D EDICATION
I dedicate this book to the sacred memory of my parents and teachers, to my wife Kamala, and to my curious daughters Meenoo, Aparajita, and Ankita.
A BSTRACT
Quantum mechanics is the most successful theory for describing the microworld of photons, atoms, and their aggregates. It is behind much of the successes of modern technology. It has deep philosophical implications to the fundamental nature of material reality. A few decades ago, it was also realized that it is connected to the computer science and information theory. With this understanding were born the new disciplines of quantum computing and quantum communication.
The current book introduces the very exciting area of quantum communication, which lies at the intersection of quantum mechanics, information theory, and atomic physics. The relevant concepts of these disciplines are explained, and their implication for the task of unbreakably secure communication is elucidated. The mathematical formulation of various approaches has been explained. An attempt has been made to keep the exposition self-contained. A senior undergraduate with good mathematics and physics background should be able to follow the current thinking about these issues after understanding the material presented in this book.
KEYWORDS
Information Theory, Quantum Mechanics, Shannon Entropy, Quantum Coding, Entanglement, Quantum Information
C ONTENTS
A CKNOWLEDGMENT
I deeply thank Dr. Ashok Goel for being the impetus behind writing this book and Dr. Kurt Jacobs for going through the manuscript.
__________________________
Communication in the form of written and spoken languages is a hallmark of human societies. Even lower life-forms and nonliving entities communicate non-linguistically. The basic building blocks of matter consist of quarks and leptons, and they communicate by exchanging the force quanta of gluons and photons respectively. Among the living entities, cells communicate via biochemical molecules. Languages are the most important communication tools on which our distinctive human societies are based. They also include nonverbal varieties like sign languages, semaphores, etc.
Still when we speak of communication in the context of technology, we actually mean telecommunication. It started with telegraphs based on Morse code, progressed through radio and wireless, and finally transformed into the Internet. Technically, communication involves transmission and reception of messages using electromagnetic waves in free space, photonic pulses in optical fiber, or currents in copper wires. Several of their attributes like currents, voltages, amplitudes, frequencies, etc., are used for carrying messages of importance to both machines and humans.
Efforts to develop a theoretical understanding of telecommunications started quite early. A very important problem was to determine the maximum amount of information that could be sent over an information channel in presence of noise. It took the genius of Claude Shannon (Shannon 1948) to solve this problem, and as a result, launch Information Theory as a distinct area of knowledge. He has earned the distinction of being the Einstein of communication. Before Shannon, the definition of information applicable to telecommunication was very qualitative. He made it more precise and quantitative using Boolean algebra and basic thermodynamic principles.
Let us assume that there is a discrete random process in which the basic event takes a finite number of values. Tossing a coin, where there are only two outcomes of either heads or tails, exemplifies such a process. The probability of obtaining k successes (heads for our example) out of n tosses is the binomial coefficient,
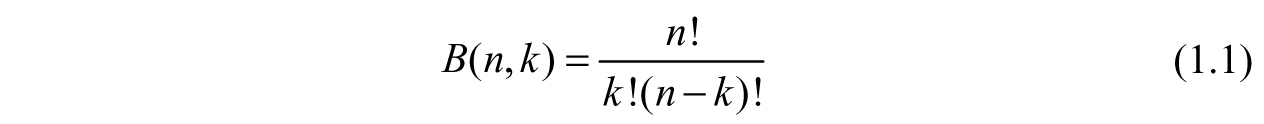
This is also known as Bernoulli process. For n , Sterlings asymptotic formula for factorials can be used to show that this process gives rise to a Gaussian distribution. In this limit the discrete variables (n, k) change into a continuous variable denoted by x.
We associate a probability p(x) (0 p(x) 1) for a random variable x(0 x ). Shannon defined information content of a random variable as a surprise function. It is a measure of how surprised we will be to find that a random variable has value x. It is defined as:
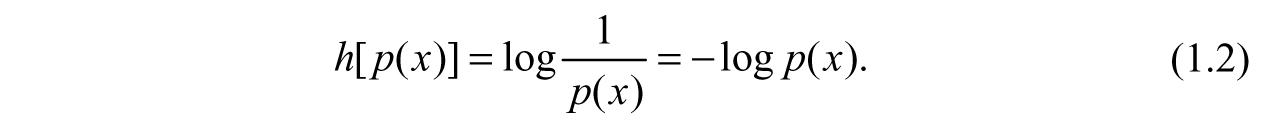
The logarithm can be in any base depending on the number of distinct and discrete values x can take. The base is 2 for the process of coin tossing. Then the Shannon entropy or information entropy is defined as the average value of the surprise function,
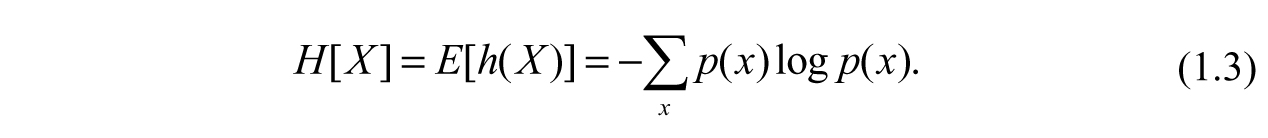
The notation E [.] denotes an estimated value,which is similar to the mean value. H [X] is a measure of disorder in the random process p(x), and the summation is over all of its possible values. For a binary random variable (head or tail in the coin example), the summation is over probability p and its complimentary (1p). This is analogous to a digital value taking value 0 or 1. Then the Shannon entropy is:
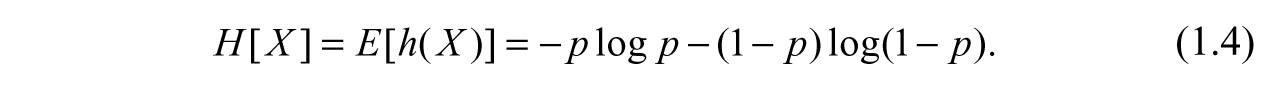
Here, the logarithm is taken to the base 2, and this entropy is measured in the units of bits. The word bit is a shortened form of binary digit. This function has mathematical properties expected from an entropy-like function well-known in Statistical Mechanics.
A given information channel is a physical medium through which information travels from source to destination in presence of noise. Capacity C (in Hz or bits/s) of such a channel is defined as the maximum rate at which this information can be transmitted. Let us assume the following about this channel.
B = Bandwidth of the channel (in Hz or bits/s)
The channel noise is Additive White Gaussian Noise (AWGN)
S/N = Signal (S) to noise (N) ratio (SNR), where S and N are signal and noise powers (in Watts or Volts2) respectively
The Shannon-Hartley theorem then states that
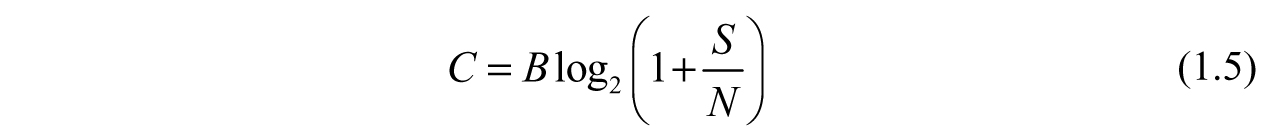
Next page