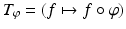Tanja Eisner, Blint Farkas, Markus Haase, and Rainer Nagel 2015
Tanja Eisner , Blint Farkas , Markus Haase and Rainer Nagel Operator Theoretic Aspects of Ergodic Theory Graduate Texts in Mathematics 10.1007/978-3-319-16898-2_1
1. What Is Ergodic Theory?
... 10 ves koromban desapm elmondta annak bizonytst, hogy vgtelen sok prmszm van, s hogy a prmszmok kztt tetszlegesen nagy hzagok vannak, gy bartsgom a prmszmokkal korn kezddtt...
Paul Erds
Ergodic Theory is not one of the classical mathematical disciplines and its name, in contrast to, e.g., number theory, does not indicate its subject. However, its origin can be described quite precisely.
It was around 1880 when Boltzmann, Maxwell, and others tried to explain thermodynamical phenomena by mechanical models and their underlying mathematical principles. In this context, Boltzmann (:
Monoden, welche nur durch die Gleichung der lebendigen Kraft beschrnkt sind, will ich als Ergoden bezeichnen.
A few years later the Ehrenfests () wrote
haben Boltzmann und Maxwell eine Klasse von mechanischen Systemen durch die folgende Forderung definiert:
Die einzelne ungestrte Bewegung des Systems fhrt bei unbegrenzter Fortsetzung schlielich durch jeden Phasenpunkt hindurch, der mit der mitgegebenen Totalenergie vertrglich ist. Ein mechanisches System, das diese Forderung erfllt, nennt Boltzmann ein ergodisches System .
The assumption that certain systems are ergodic is then called Ergodic Hypothesis. Leaving the original problem behind, Ergodic Theory set out on its fascinating journey into mathematics and arrived at quite unexpected destinations.
Before we, too, undertake this journey, let us explain the original problem without going too deep into the underlying physics. We start with an (ideal) gas contained in a box and represented by d (frictionlessly) moving particles. Each particle is described by six coordinates (three for position, three for velocity), so the situation of the gas (better: the state of the system) is given by a point
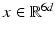
. Clearly, not all points in
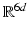
can be attained by our gas in the box, so we restrict our considerations to the set X of all possible states and call this set the state space of our system. We now observe that our system changes while time is running, i.e., the particles are moving (in the box) and therefore a given state (= point in X ) also moves (in X ). This motion (in the box, therefore in X ) is governed by Newtons laws of mechanics and then by Hamiltons differential equations. The solutions to these equations determine a map
in the following way: If our system, at time t =0, is in the state x 0 X , then at time t =1 it will be in a new state x 1, and we define
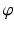
by
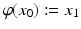
. As a consequence, at time t =2 the state x 0 becomes
and
at time
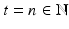
. The so-obtained set
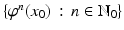
of states is called the orbit of x 0. In this way, the physical motion of the system of particles becomes a motion of the points in the state space. The motion of all states within one time unit is given by the map
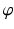
. For these objects we introduce the following terminology.
Definition 1.1.
A pair
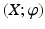
consisting of a state space X and a map
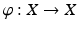
is called a dynamical system .
The mathematical goal now is not so much to determine
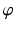
but rather to find interesting properties of it. Motivated by the underlying physical situation, the emphasis is on long term properties of
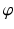
, i.e., properties of
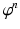
as n gets large.
First Objection. In the physical situation it is not possible to determine exactly the given initial state x 0 X of the system or any of its later states
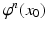
(Figure ).
Fig. 1.1
Try to determine the exact state of the system for only d =1 000 gas particles
To overcome this objection we introduce observables, i.e., functions
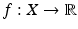
assigning to each state x X the value f ( x ) of a measurement, for instance of the temperature. The motion in time (evolution) of the states described by the map
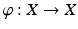
is then reflected by a map
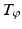
of the observables defined as
and called the Koopman operator . This change of perspective is not only physically justified, but it also has an enormous mathematical advantage:
The set of all observables
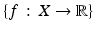
has a vector space structure and the map
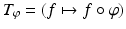

![Eisner Tanja Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)










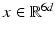 . Clearly, not all points in
. Clearly, not all points in 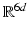 can be attained by our gas in the box, so we restrict our considerations to the set X of all possible states and call this set the state space of our system. We now observe that our system changes while time is running, i.e., the particles are moving (in the box) and therefore a given state (= point in X ) also moves (in X ). This motion (in the box, therefore in X ) is governed by Newtons laws of mechanics and then by Hamiltons differential equations. The solutions to these equations determine a map
can be attained by our gas in the box, so we restrict our considerations to the set X of all possible states and call this set the state space of our system. We now observe that our system changes while time is running, i.e., the particles are moving (in the box) and therefore a given state (= point in X ) also moves (in X ). This motion (in the box, therefore in X ) is governed by Newtons laws of mechanics and then by Hamiltons differential equations. The solutions to these equations determine a map 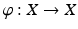
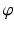 by
by 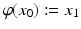 . As a consequence, at time t =2 the state x 0 becomes
. As a consequence, at time t =2 the state x 0 becomes 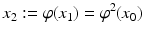
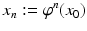
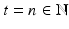 . The so-obtained set
. The so-obtained set 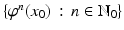 of states is called the orbit of x 0. In this way, the physical motion of the system of particles becomes a motion of the points in the state space. The motion of all states within one time unit is given by the map
of states is called the orbit of x 0. In this way, the physical motion of the system of particles becomes a motion of the points in the state space. The motion of all states within one time unit is given by the map 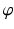 . For these objects we introduce the following terminology.
. For these objects we introduce the following terminology.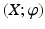 consisting of a state space X and a map
consisting of a state space X and a map 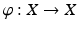 is called a dynamical system .
is called a dynamical system .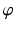 but rather to find interesting properties of it. Motivated by the underlying physical situation, the emphasis is on long term properties of
but rather to find interesting properties of it. Motivated by the underlying physical situation, the emphasis is on long term properties of 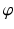 , i.e., properties of
, i.e., properties of 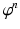 as n gets large.
as n gets large.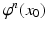 (Figure ).
(Figure ). 
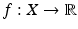 assigning to each state x X the value f ( x ) of a measurement, for instance of the temperature. The motion in time (evolution) of the states described by the map
assigning to each state x X the value f ( x ) of a measurement, for instance of the temperature. The motion in time (evolution) of the states described by the map 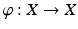 is then reflected by a map
is then reflected by a map 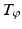 of the observables defined as
of the observables defined as 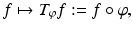
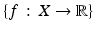 has a vector space structure and the map
has a vector space structure and the map