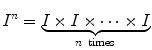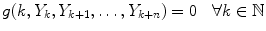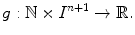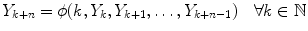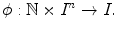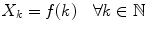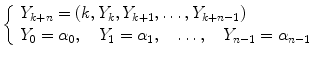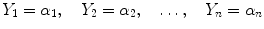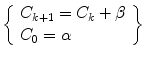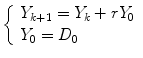1.1 1.1 Definitions and notation
In the sequel we will consider sequences of complex numbers. A sequence is a function F : , where = {0,1,2,3,}.
The reader not familiar with complex numbers can, at a first reading, replace with . For convenience the basic properties of complex numbers are recalled in Appendix B.
A generic sequence will be indicated with a capital letter, for example F, while its k -th term will be denoted with a capital letter with a subscript, F k . In other words F k = F ( k ).
Following a common practice, we will identify a sequence F with the ordered set of values it takes: F = {F k } k or, briefly F = {F k }.
Although the student interested in the description of variables in a succession of steps or temporal instants may find it restrictive to deal only with functions defined on the set of natural numbers, this is not the case. In fact, if t 0 is any initial instant and h > 0 is an increment, the sequence {t 0 , t 0 + h, t 0 + 2 h , t 0 + 3 h,} is mapped one-to-one to the sequence {0,1,2,3 ,} by the transformation
Since the object of our study are quantities that depend on natural numbers, it is not surprising that the induction principle, recalled below, turns out to be very useful for the analysis:
Let P (k) be a proposition about the natural number k. If:
i)
there exists
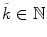
such that
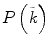
is true;
ii)
for all
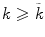
, if P (k) is true, then P (k + 1) is true;
then the proposition P (k) is true for all

.
For any subset I of (in most cases I will be an interval in ), we set:
i.e. I n denotes the set of the n -tuples ( x 1 , x 2 ,, x n ) such that x j I for all j = 1,2 , ,n .
Definition 1.1. We call difference equation of order n, the set of equations
where n is a positive integer and g is a given scalar function in n+2 variables, defined on I n +1
A difference equation of order n is said to be in normal form if it is expressed in the form
where is a given function
Formula is a recursive relationship that starting from the knowledge of the first k consecutive values of the sequence Y allows, with a lot of patience, to evaluate step by step all values of the sequence. In many cases, this calculation can be prohibitive even with automatic procedures. Hence, it is useful to know an explicit formula (say, a non-recursive one) for Y.
Definition 1.2. A solution of is a sequence X e xplicitly defined via
where f : I is a given function that renders an identity when f (k) replaces Y k , for any k .
The set of all solutions of is called general solution of the equation.
Theorem 1.3 (existence and uniqueness) . If is a function as in has solutions .
For each choice of the n-tuple ( 0, 1 ,, n 1) I n , the problem with initial data associated with the difference equation in normal form :
has a unique solution.
Proof. By substituting the initial conditions 0 , 1 , , n 1 in , ( 1 , 2 , , n 1 , n ) belongs to I n : substituting the conditions
in equation .
When it is not possible to find an explicit expression for the solution X, it is still useful to show whether the sequence X exhibits a particular property or not: periodicity, asymptotic behavior to a certain value, or even a more complex trend.
1.2 1.2 Examples
In this section we give motivations for the study of discrete mathematical models through the discussion of some examples. Their systematic analysis is deferred to later chapters.
The first examples are basic. They are presented in an increasing order of difficulty and they are grouped by subject. The last examples, not elementary and quite technical at first sight, are intended to illustrate the variety of situations in which difference equations play an important role in applied mathematics.
Example 1.4. A mobile phone call costs as connection charge and for each minute of conversation. The total cost of call C k +1 after k + 1 minutes of conversation is the solution of
which is an example of a problem with initial data for a difference equation of the first order.
Example 1.5 (Simple interest). Suppose that the amount Y k +1 of a deposit of money calculated at time k+ 1 (the date for the computation of the interests) is given by the amount Y k of the preceding time plus the interest calculated on the basis of a constant rate r on the initial deposit D 0. The difference model describing the behavior of the deposit corresponds to the problem:









![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)


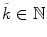 such that
such that 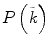 is true;
is true;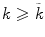 , if P (k) is true, then P (k + 1) is true;
, if P (k) is true, then P (k + 1) is true; .
.