Let us start off with an excerpt from the introduction to Chapter V in What is mathematics? by R. Courant and H. Robbins.
In the middle of the nineteenth century there began a completely new development in geometry that was soon to become one of the great forces in modern mathematics. The new subject, called analysis situs or topology, has as its object the study of the properties of geometrical figures that persist even when the figures are subjected to deformations so drastic that all their metric and projective properties are lost. (...) When Bernhard Riemann (18261866) came to Gttingen as a student, he found the mathematical atmosphere of that university town filled with keen interest in these strange new geometrical ideas. Soon he realized that here was the key to the understanding of the deepest properties of analytic functions of a complex variable.
The expression deformations so drastic is rather vague, and as a matter of fact modern topology studies several classes of transformations of geometrical figures, the most important among which are homeomorphisms and homotopy equivalences .
While precise definitions for these will be given later, in this chapter we shall encounter a preliminary, and only partial notion of homeomorphism, and discuss a few examples. We will stay away from excessively rigorous definitions and proofs at this early stage, and try instead to rely on the geometrical intuition of the reader, with the hope that in this way we might help newcomers acquire the basic ideas.
1.1 A Bicycle Ride Through the Streets of Rome
Problem 1.1
On a bright Sunday morning Mr. B. decides to go on a bike ride that crosses every bridge in Rome once, and only once . Knowing that he can decide where to start from and where to end, will Mr. B. be able to accomplish his wish?
We remind those who arent familiar with the topography of Rome that the city is divided by the river Tiber and its affluent Aniene in four regions, one being the Tiberine island, lying in the middle of the river and joined to either riverbank by bridges.
In order to answer the question we neednt go around the streets of Rome on two wheels testing possibilities, nor mess up a street map with a marker.
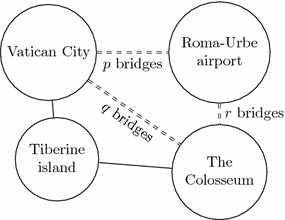
The problem can be visualised by drawing four circles on a sheet of paper, one for each region, and indicating how many bridges connect any two regions (Fig. ).
Fig. 1.1
The topology of the bridges of Rome
A configuration of this kind contains all the information we need to solve the problem. If you agree with this statement, then you are thinking topologically . In other words you have understood that whether the proposed bicycle ride is possible doesnt depend on metric or projective properties like the bridges length, their architectural structure, the extension of mainland areas and so on. But if you insist on solving the problem using a street map, you should imagine the map is drawn on a thin rubber sheet. Think of stretching, twisting and rumpling it, as much as you like, without tearing it nor making different points touch one another by folding: you will agree that the answer stays the same.
Problem 1.2
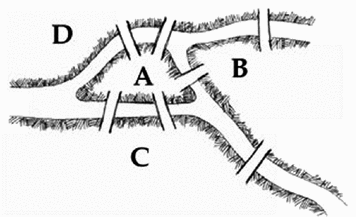
In the old town of Knigsberg, on the river Pregel, there are two islets and seven bridges as in Fig.. The story goes that Mr. C. wanted to cross on foot every bridge in Knigsberg only once , and could start and finish his walk at any point. Would have Mr. C. been able to do so?
Fig. 1.2
The bridges of old Knigsberg
Heres another problem of topological flavour:
Problem 1.3
Can one drive from Rome to Venice by never leaving the motorway?
As the motorway goes through Rome and Venice, the problem is truly a question about the connectedness of the Italian road system: a network of roads is connected if one can drive from any one point to any other. Here, too, the answer is clearly independent of how long the single stretches of road are, or how many turns or slopes there are etc.
A useful mathematical concept for solving the previous problems is that of a graph . In Euclidean space a graph is a non-empty set of
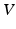
points, called nodes or vertices , certain pairs of which are joined by
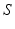
segments called edges . Edges are not necessarily straight, but can be parts of circles, parabolas, ellipses, or more generally regular arcs that do not pass through the same point in space more than once. Another assumption is that distinct edges meet only at nodes. A walk of length
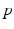
in a graph is a sequence
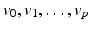
of nodes and a sequence
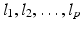
of edges, with
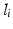
joining
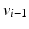
to
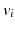
for any
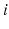
. The nodes
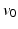
and
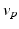
are the endpoints of the walk. A graph is said to be connected if there is a walk beginning and ending at any two given nodes
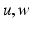
.
If
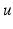
is a node in a graph
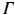
, we call degree of
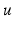
in
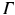
the number of edges containing
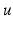
, counting twice edges with both endpoints in
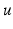
. Its straightforward that the sum of the degrees of all nodes equals twice the number of edges; in particular, any graph must have an even number of odd-degree nodes.
A graph is called Eulerian if theres a walk that visits each edge exactly once: in this case the length of the walk equals the number of edges in the graph.














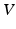 points, called nodes or vertices , certain pairs of which are joined by
points, called nodes or vertices , certain pairs of which are joined by 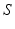 segments called edges . Edges are not necessarily straight, but can be parts of circles, parabolas, ellipses, or more generally regular arcs that do not pass through the same point in space more than once. Another assumption is that distinct edges meet only at nodes. A walk of length
segments called edges . Edges are not necessarily straight, but can be parts of circles, parabolas, ellipses, or more generally regular arcs that do not pass through the same point in space more than once. Another assumption is that distinct edges meet only at nodes. A walk of length 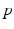 in a graph is a sequence
in a graph is a sequence 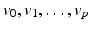 of nodes and a sequence
of nodes and a sequence 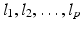 of edges, with
of edges, with 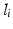 joining
joining 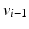 to
to 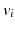 for any
for any 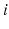 . The nodes
. The nodes 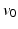 and
and 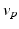 are the endpoints of the walk. A graph is said to be connected if there is a walk beginning and ending at any two given nodes
are the endpoints of the walk. A graph is said to be connected if there is a walk beginning and ending at any two given nodes 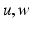 .
.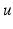 is a node in a graph
is a node in a graph 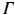 , we call degree of
, we call degree of 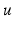 in
in 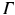 the number of edges containing
the number of edges containing 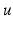 , counting twice edges with both endpoints in
, counting twice edges with both endpoints in 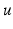 . Its straightforward that the sum of the degrees of all nodes equals twice the number of edges; in particular, any graph must have an even number of odd-degree nodes.
. Its straightforward that the sum of the degrees of all nodes equals twice the number of edges; in particular, any graph must have an even number of odd-degree nodes.