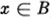Introduction to Topology
Introduction to Topology
Third Edition
by Bert Mendelson
DOVER PUBLICATIONS, INC.
NEW YORK
Copyright
Copyright 1962, 1968, 1975 by Marion Mendelson.
Copyright renewed 1990 by Marion Mendelson.
All rights reserved.
Bibliographical Note
This Dover edition, first published in 1990, is an unabridged, unaltered republication of the work originally published by Allyn and Bacon, Inc., Boston, 1975 (First Edition, 1962; Second Edition, 1968).
Library of Congress Cataloging-in-Publication Data
Mendelson, Bert, 19261988
Introduction to topology / by Bert Mendelson. 3rd ed.
p. cm.
Unabridged, unaltered republication of the work originally published by Allyn and Bacon, Inc., Boston, 1975T.p. verso.
Includes bibliographical references (p. ).
ISBN-13: 978-0-486-66352-4
ISBN-10: 0-486-66352-3
1. Topology. I. Title.
[QA611.M39 1990]
CIP
Manufactured in the United States by Courier Corporation
66352313
www.doverpublications.com
Contents
Preface to the Third Edition
The first edition of this text was based on lecture notes prepared for a one-semester undergraduate course given at Smith College. The aim was to present a simple, thorough survey of elementary topics to students whose preparation included a calculus sequence in which some attention had been paid to definitions and proofs of theorems. With this in mind, I have attempted to resist the temptation to include more topics. There are many excellent introductory topology texts which are first-year graduate school level texts and it was not my original intention, nor is it now, to write at that level.
The main outlines of the text have not been changed. The first chapter is an informal discussion of set theory. The concept of countability has been postponed until , where it appears in the context of compactness.
The second chapter is a discussion of metric spaces. The topological terms open set, neighborhood, etc., are introduced. Particular attention is paid to various distance functions which may be defined on Euclidean n-space and which lead to the ordinary topology.
In taking up topological spaces in , the transition from the particular to the general has been maintained, so that the concept of topological space is viewed as a generalization of the concept of metric space. Thus there is a similarity or, perhaps, a redundancy in the presentation of these two topics. A great deal of attention has been paid to alternate procedures for the creation of a topological space, using neighborhoods, etc., in the hope that this seemingly trivial, but subtle, point would be clarified.
are devoted to a discussion of the two most important topological properties: connectedness and compactness. Some of this material could lead to further discussion of topics related to analysis, function spaces, separation axioms, metrization theorems, to name a few. On the other hand, material such as homotopy and two-dimensional closed surfaces could lead to further discussion of topics related to algebraic topology.
In conclusion, it is a pleasure to express in print my gratitude to those mathematicians under whom I studied and who helped make this book possible. In particular I should like to mention Professors C. Chevalley, S. Eilenberg, I. James, H. Riberio, P. Smith, and E. Thomas.
B. M.
CHAPTER
Theory of Sets
1 INTRODUCTION
As in any other branch of mathematics today, topology consists of the study of collections of objects that possess a mathematical structure. This remark should not be construed as an attempt to define mathematics, especially since the phrase mathematical structure is itself a vague term. We may, however, illustrate this point by an example.
The set of positive integers or natural numbers is a collection of objects N on which there is defined a function s, called the successor function, satisfying the conditions:
1. For each object x in N, there is one and only one object y in N such that y = s(x);
2. Given objects x and y in S such that s(x) = s(y), then x = y;
3. There is one and only one object in N, denoted by 1, which is not the successor of an object in N, i.e., 1 s(x) for each x in N;
4. Given a collection T of objects in N such that 1 is in T and for each x in T, s(x) is also in T, then T = N.
The four conditions enumerated above are referred to as Peanos axioms for the natural numbers. The fourth condition is called the principle of mathematical induction. One defines addition of natural numbers in such a manner that s(x) = x + 1, for each x in N, which explains the use of the word successor for the function s. What is significant at the moment is the conception of the natural numbers as constituting a certain collection of objects N with an additional mathematical structure, namely the function s.
We shall describe a topological space in the same terms, that is, a collection of objects together with a specified structure. A topological space is a collection of objects (these objects usually being referred to as points), and a structure that endows this collection of points with some coherence, in the sense that we may speak of nearby points or points that in some sense are close together. This structure can be prescribed by means of a collection of subcollections of points called open sets. As we shall see, the major use of the concept of a topological space is that it provides us with an exact, yet exceedingly general setting for discussions that involve the concept of continuity.
By now the point should have been made that topology, as well as other branches of mathematics, is concerned with the study of collections of objects with certain prescribed structures. We therefore begin the study of topology by first studying collections of objects, or, as we shall call them, sets.
2 SETS AND SUBSETS
We shall assume that the terms object, set, and the relation is a member of are familiar concepts. We shall be concerned with using these concepts in a manner that is in agreement with the ordinary usage of these terms.
If an object A belongs to a set S we shall write 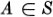 (read, A in S). If an object A does not belong to a set S we shall write
(read, A in S). If an object A does not belong to a set S we shall write 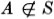 (read, A not in S). If A1,... , An are objects, the set consisting of precisely these objects will be written {A1,... , An}. For purposes of logical precision it is often necessary to distinguish the set {A}, consisting of precisely one object A, from the object A itself. Thus
(read, A not in S). If A1,... , An are objects, the set consisting of precisely these objects will be written {A1,... , An}. For purposes of logical precision it is often necessary to distinguish the set {A}, consisting of precisely one object A, from the object A itself. Thus  is a true statement, whereas A = {A} is a false statement. It is also necessary that there be a set that has no members, the so-called null or empty set. The symbol for this set is .
is a true statement, whereas A = {A} is a false statement. It is also necessary that there be a set that has no members, the so-called null or empty set. The symbol for this set is .
Let A and B be sets. If for each object 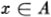 , it is true that
, it is true that 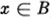
Next page













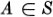 (read, A in S). If an object A does not belong to a set S we shall write
(read, A in S). If an object A does not belong to a set S we shall write 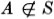 (read, A not in S). If A1,... , An are objects, the set consisting of precisely these objects will be written {A1,... , An}. For purposes of logical precision it is often necessary to distinguish the set {A}, consisting of precisely one object A, from the object A itself. Thus
(read, A not in S). If A1,... , An are objects, the set consisting of precisely these objects will be written {A1,... , An}. For purposes of logical precision it is often necessary to distinguish the set {A}, consisting of precisely one object A, from the object A itself. Thus  is a true statement, whereas A = {A} is a false statement. It is also necessary that there be a set that has no members, the so-called null or empty set. The symbol for this set is .
is a true statement, whereas A = {A} is a false statement. It is also necessary that there be a set that has no members, the so-called null or empty set. The symbol for this set is .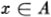 , it is true that
, it is true that