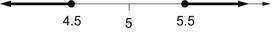Peter D. Lax and Maria Shea Terrell Undergraduate Texts in Mathematics Calculus With Applications 2nd ed. 2014 10.1007/978-1-4614-7946-8_1 Springer Science+Business Media New York 2014
1. Numbers and Limits
1.1 Inequalities
One cannot exaggerate the importance in calculus of inequalities between numbers. Inequalities are at the heart of the basic notion of convergence, an idea central to calculus. Inequalities can be used to prove the equality of two numbers by showing that one is neither less than nor greater than the other. For example, Archimedes showed that the area of a circle was neither less than nor greater than the area of a triangle with base the circumference and height the radius of the circle.
A different use of inequalities is descriptive. Sets of numbers described by inequalities can be visualized on the number line.
To say that a is less than b , denoted by a < b , means that b a is positive. On the number line in Fig., a would lie to the left of b . Inequalities are often used to describe intervals of numbers. The numbers that satisfy a < x < b are the numbers between a and b , not including the endpoints a and b . This is an example of an open interval, which is indicated by round brackets, ( a , b ).
To say that a is less than or equal to b , denoted by a b , means that b a is not negative. The numbers that satisfy a x b are the numbers between a and b , including the endpoints a and b . This is an example of a closed interval, which is indicated by square brackets, [ a , b ]. Intervals that include one endpoint but not the other are called half-open or half-closed . For example, the interval a < x b is denoted by ( a , b ] (Fig.).
Fig. 1.2
Left : the open interval ( a , b ). Center : the half open interval ( a , b ]. Right : the closed interval [ a , b ]
The absolute value| a |of a number a is the distance of a from 0; for a positive, then,| a |= a , while for a negative,
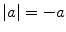
. The absolute value of a difference,| a b |, can be interpreted as the distance between a and b on the number line, or as the length of the interval between a and b (Fig. ).
Fig. 1.3
Distances are measured using absolute value
The inequality
can be interpreted as stating that the distance between a and b on the number line is less than . It also means that the difference between a and b is no more than and no less than:
In Problem 1.9, we ask you to use some of the properties of inequalities stated in Sect.).
Example 1.1.
The inequality
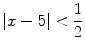
describes the numbers x whose distance from 5 is less than
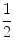
. This is the open interval (4.5,5.5). It also tells us that the difference x 5 is between
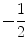
and
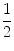
. See Fig.. The inequality
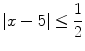
describes the closed interval [4.5,5.5].
Fig. 1.4
Left : the numbers specified by the inequality
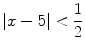
in Example 1.1. Right : the difference x 5 is between
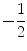
and
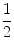
The inequality
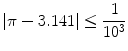
can be interpreted as a statement about the precision of 3.141 as an approximation of . It tells us that 3.141 is within
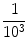
of , and that is in an interval centered at 3.141 of length
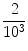
.
Fig. 1.5
Approximations to
We can imagine smaller intervals contained inside the larger one in Fig..
We use ( a ,) to denote the set of numbers that are greater than a , and [ a ,) to denote the set of numbers that are greater than or equal to a . Similarly, (, a ) denotes the set of numbers less than a , and (, a ] denotes those less than or equal to a . See Fig..
Fig. 1.6
The intervals (, a ), (, a ], [ a ,), and ( a ,) are shown from left to right
Example 1.2.
The inequality
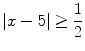
describes the numbers whose distance from 5 is greater than or equal to
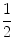
. These are the numbers that are in (,4.5] or in [5.5,). See Fig..
Fig. 1.7
The numbers specified by the inequality in Example 1.2
1.1a Rules for Inequalities










![Chris Monahan [Chris Monahan] - Calculus II](/uploads/posts/book/119088/thumbs/chris-monahan-chris-monahan-calculus-ii.jpg)


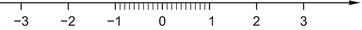

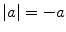 . The absolute value of a difference,| a b |, can be interpreted as the distance between a and b on the number line, or as the length of the interval between a and b (Fig. ).
. The absolute value of a difference,| a b |, can be interpreted as the distance between a and b on the number line, or as the length of the interval between a and b (Fig. ).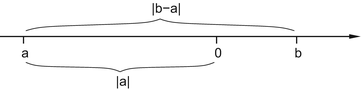
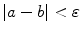
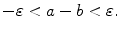
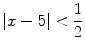 describes the numbers x whose distance from 5 is less than
describes the numbers x whose distance from 5 is less than 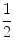 . This is the open interval (4.5,5.5). It also tells us that the difference x 5 is between
. This is the open interval (4.5,5.5). It also tells us that the difference x 5 is between 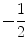 and
and 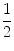 . See Fig.. The inequality
. See Fig.. The inequality 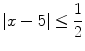 describes the closed interval [4.5,5.5].
describes the closed interval [4.5,5.5].
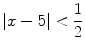 in Example 1.1. Right : the difference x 5 is between
in Example 1.1. Right : the difference x 5 is between 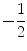 and
and 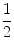
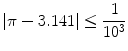 can be interpreted as a statement about the precision of 3.141 as an approximation of . It tells us that 3.141 is within
can be interpreted as a statement about the precision of 3.141 as an approximation of . It tells us that 3.141 is within 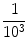 of , and that is in an interval centered at 3.141 of length
of , and that is in an interval centered at 3.141 of length 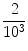 .
.
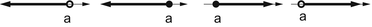
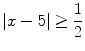 describes the numbers whose distance from 5 is greater than or equal to
describes the numbers whose distance from 5 is greater than or equal to 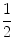 . These are the numbers that are in (,4.5] or in [5.5,). See Fig..
. These are the numbers that are in (,4.5] or in [5.5,). See Fig..