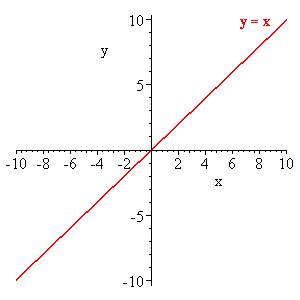calculus with applications (MIT 18.013A)
From: https://ocw.mit.edu/ans7870/18/18.013a/textbook/HTML/index.html
Chapter 1: Philosophy, Numbers and Functions
Introduction
We consider the basic context in which our efforts will be concentrated: the realms of numbers and functions. We describe "standard functions" which are those that will appear most often in your world, and inverse functions
Topics
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.1 Philosophy
We will not dwell on philosophy but merely list some features we hope to encorporate in the course.
Philosophy of the Course
1. Use computers as much as possible.
2. Use spreadsheets.
3. Encourage active learning rather than passive; try to make you think about the material.
4. Integrate one variable calculus into multivariable calculus so that they are treated together rather than one after the other.
5. Ask you to submit homework electronically via email to me when appropriate.
6. Make you redo homework until it is correct.
7. Feedback an important part of required activity.
Philosophy of Learning
1. Amount learned is proportional to time put in.
2. Best way to learn is to figure out ideas yourself or teach them to someone else.
3. Second best is to do so with hints from others like your friends or us.
4. Third best is to get the ideas from reading; but pause in your reading to think about them.
5. Fourth best: unacceptable: don't get them at all.
6. The object of a lecture is not so much to inform you of important facts, but rather to stimulate you to try to learn about some concept.
7. The object of the course is to empower you to use the concepts of calculus in any context.
1.2 Numbers
We start with the basic concept of a number. The Natural Numbers, denoted as N, are the numbers 1,2,3,... These are closed under Addition.
A set that can be put inwith N or a subset of N is called countable.
Introducing the notion of subtraction makes us enlarge N to get the Integers, denoted as Z, positive or negative or 0, so that our numbers are closed under the operation of substraction.
Exercise 1.1 Is Z countable?
Z is closed under multiplication; which is to say that the product of two integers is an integer.
To obtain a set of numbers closed under Division: we must enlarge Z to get the Rational Numbers Q, which are fractions of the form 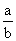 where a is in Z and b is in N.
where a is in Z and b is in N.
Exercises:
1.2 Is Q countable? (See picture for hint.)
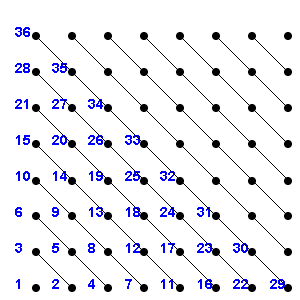
1.3 Prove or disprove: a countable set of countable sets is countable.
Decimal form of numbers
The numbers between 0 and 1 can each be represented as a decimal point followed by an infinite string of digits, each digit being one of 1, 2, 3, ..., 9, 0.
Rational numbers repeat themselves endlessly after some point: (for example 1 / 4 is .250* or also .249* where the star means that you repeat the starred digit endlessly) 1 / 3 is .3*, 1 / 7 = .(142857)*, 57 / 100 = .570*.
Irrational numbers do not do so.
Exercises:
1.4 Prove that rational numbers repeat the same finite sequence of digits endlessly, and that irrational numbers do not.
1.5 Are there non-rational decimal digit sequences?
1.6 Are all such sequences countable? (See picture for hint.)
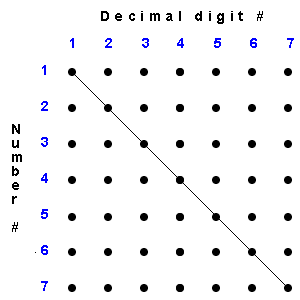
A number which differs from the number in the k-th position on the list in its k-th decimal digit, cannot be in any position on the list of numbers!
Algebraic numbers are solutions to polynomial equations, with integer coefficients.
Exercise 1.7 Are algebraic numbers countable?
The Real Numbers R are all distinct infinite sequences of digits, having a sign and a finite number of digits in front of the decimal point.
You can add subtract multiply and divide them except dividing by 0 is not allowed.
Are there other sets that we might dignify by calling numbers?
Yes! There are "Numbers mod x". These are remainders of Z or Q or R obtained when you divide by x.
There are also complex numbers, which form the set C. These are expressions of the form a + ib where i2 = -1, a and b are in R, and multiplication and division are as in R with the additional rule above.
1.3 Functions
A Set is a primitive notion. We start with set (or another word for it: collection) as a basic notion.
An Ordered Countable Set is also called a sequence. 1, 2, 3, ... is a sequence.
If it has two elements it is called an ordered pair. (3, 4) is such a pair.
A function is a collection of ordered pairs whose first elements are all different.
The first elements are called arguments the second values.
The set of arguments is called its domain.
The set of values is called its range.
We describe each pair in the function f by f(argument) = value.
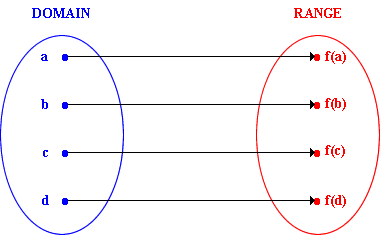
It is perfectly OK for f to have the same value for two different arguments: say for f(d) and f(e) to be identical.
We can describe a function by listing its pairs, or by drawing a graph of representative pairs in the usual way: if f(a) = bput a point at the intersection of the vertical line through a on the x axis and the horizontal line through b on the y axis.
However we cannot list all the pairs in any function having an infinite or huge domain.
Instead we define such a function by giving a procedure you can use to construct its value for any argument you choose in its domain. This procedure is often called a "formula" for the function.
1.4 Standard Functions
A standard function is one defined on an interval of R that is obtained by a finite sequence of standard operations starting from any combination of three basic functions.
What are the basic functions?
The identity function f(x) = x
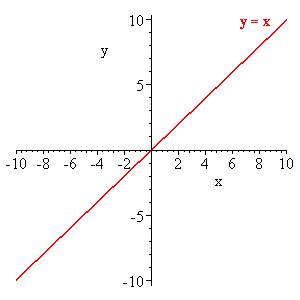
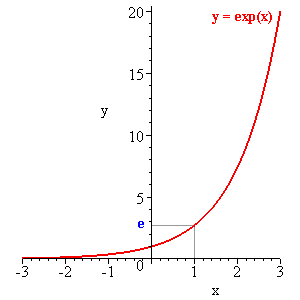
Thef(x) = exp(x)
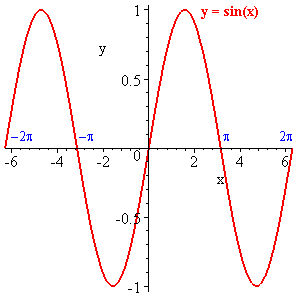
Thef(x) = sin(x)
What are the standard operations?
Multiplication by a number in R, addition, subtraction, multiplication, division, substitution of the value of one function as argument of another, and taking the "inverse".
Most of the functions we encounter will be standard functions.


















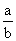 where a is in Z and b is in N.
where a is in Z and b is in N.