
 Copyright
Copyright Copyright 2020 by Jerrold Franklin All rights reserved.
Bibliographical NoteUnderstanding Vector Calculus: Practical Development and Solved Problems is a new work, first published by Dover Publications, Inc., in 2020.
International Standard Book NumberISBN-13: 978-0-486-83590-7ISBN-10: 0-486-83590-1 Manufactured in the United States by LSC Communications 83590101 www.doverpublications.com 2 4 6 8 10 9 7 5 3 1 2020
ContentsPreface My purpose in this development of vector calculus is to present it in a way that will prove useful to you for the rest of your career in science or mathematics. You can think of this presentation as a workbook for learning how to use vector calculus in practical calculations and derivations. After studying the text and doing the problems, you should not have to memorize long equations or need to look anything up while you work in your field. I want you to get to the point where you can treat the use of vector calculus on the same level as you would simple algebraic calculations, working them out as you go.
The necessary background for using this book is just a knowledge of one-dimensional differential and integral calculus. Having had a multivariable calculus course is unnecessary because the multivariable aspect of vector calculus will be developed from scratch. In fact, you might have to unlearn some of the things covered in a multivariable calculus course if it relied too much on using coordinate systems, rather than the vector methods we will introduce. Although the examples in the book are usually related to physical examples, particularly electromagnetism, it is not necessary to have any background in physics. If any of the physics is new to you, you can simply disregard it and concentrate on the mathematics. On the other hand, if you have a background in (relatively simple) physics, I think you will find the references to physics of interest.
In treating electromagnetism, we use what are sometimes called natural units in which the potential of a point charge q is given by q/r. In this way, we avoid the introduction of artificial constants that might complicate the mathematics. The book has two parts. Part one is a brief text developing vector calculus from the very beginning, and then including some more detailed applications. Part two consists of answered problems, which are all closely related to the development of vector calculus in the text. Although there are answers immediately following each problem, you should not be too quick to use the answer as a crutch.
For problems that involve working through a calculation, please try your hardest to do it on your own. Then you can use the answer to check your result, or possibly see another way of doing the problem. If you go immediately to the answer, you will be learning about vector calculus, but not how to use vector calculus. Of course, if you dont see how to start, or run into a roadblock, the answer is there to help you. In any event, I hope you find my treatment interesting, perhaps entertaining, and above all, useful. I think you will see that you have nothing to fear from vector calculus, and that it will prove to be a good friend for the rest of your life.
Feel free to use me as a resource, either by answering questions you might have about the material in the book, or about anything else. You can contact me at .  Chapter 1Vector Differential Operators.1Gradient A scalar field (that is, a scalar function of the position vector r) is conveniently pictured by means of surfaces (in three dimensions) or lines (in two dimensions) along which its magnitude is constant. Depending on the physical application, these constant magnitude surfaces or lines could be called equipotentials, isobars, isotherms, or whatever applies in the given situation. A common example, shown in , is a topographic map of a hillside.
Chapter 1Vector Differential Operators.1Gradient A scalar field (that is, a scalar function of the position vector r) is conveniently pictured by means of surfaces (in three dimensions) or lines (in two dimensions) along which its magnitude is constant. Depending on the physical application, these constant magnitude surfaces or lines could be called equipotentials, isobars, isotherms, or whatever applies in the given situation. A common example, shown in , is a topographic map of a hillside.
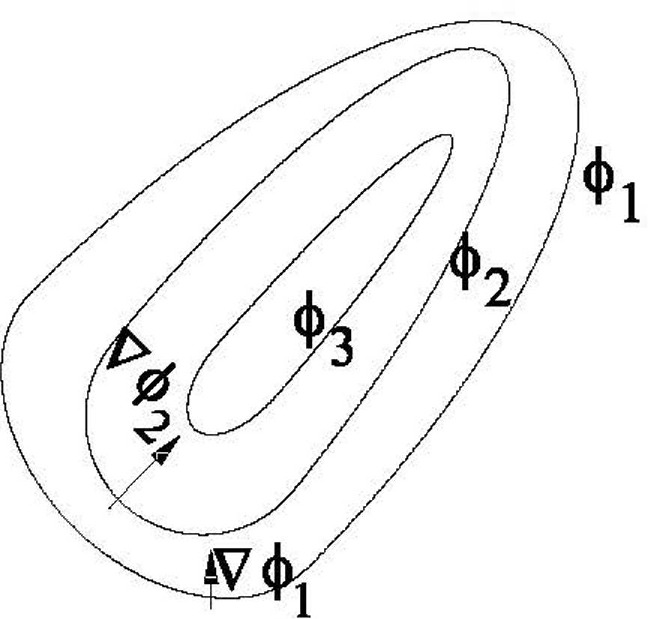
Figure 1.1: Equipotentials
i and gradients
i.
The lines of equal altitude shown on the map are equipotentials of the gravitational field. No work is done in moving along an equipotential, and the direction of steepest slope is everywhere perpendicular to the equipotential. That perpendicular direction is defined as the direction of the gradient of the potential. In our topographic example, this direction is the steepest direction up the hill. Experimentally, this would be opposite to the direction a ball would roll if placed at rest on the hillside. The magnitude of the gradient is defined to be the rate of change of the potential with respect to distance in the direction of maximum increase.
This provides a mathematical definition of the gradient as 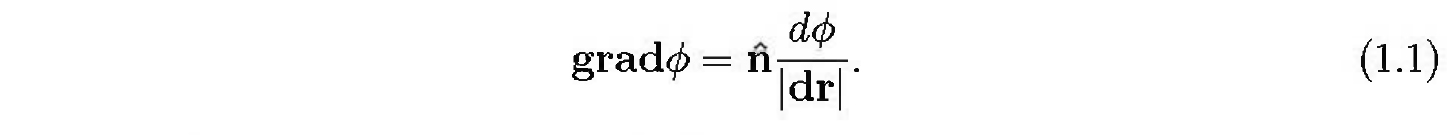 In Eq. (1.1), the unit vector
In Eq. (1.1), the unit vector 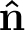 (=n/|n|) is in the direction of maximum increase of , and dr is taken in that direction of maximum increase. For infinitesimal displacements, an equipotential surface can be approximated by its tangent plane (or tangent line in two dimensions), so the change in a scalar field in an infinitesimal displacement dr will vary as the cosine of the angle between the direction of maximum gradient and dr. Then the differential change of in any direction is given by
(=n/|n|) is in the direction of maximum increase of , and dr is taken in that direction of maximum increase. For infinitesimal displacements, an equipotential surface can be approximated by its tangent plane (or tangent line in two dimensions), so the change in a scalar field in an infinitesimal displacement dr will vary as the cosine of the angle between the direction of maximum gradient and dr. Then the differential change of in any direction is given by 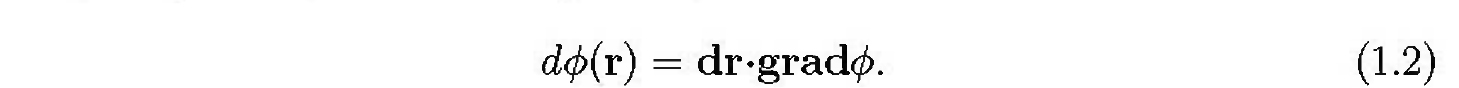 This relation can be considered an alternate definition of the gradient. The rate of change of a scalar field in a general direction a, not necessarily the direction of maximum change, can be defined by choosing dr in that direction and dividing both sides of Eq. (1.2) by the magnitude |dr|.
This relation can be considered an alternate definition of the gradient. The rate of change of a scalar field in a general direction a, not necessarily the direction of maximum change, can be defined by choosing dr in that direction and dividing both sides of Eq. (1.2) by the magnitude |dr|.
This is called the directional derivative of , defined by grad for the rate of change of in the direction . We see that grad is a vector derivative of the scalar function . However, the operation by grad has more general applications. For this reason, we introduce it as a vector differential operator, which we denote as (pronounced del). The actual calculation of can be made using a coordinate system, but it is usually better to use the definition of the gradient in Eq. (1.1) or (1.2) to find it for various functions of the position vector r directly.
We start with r(= |r|), the magnitude of r, treated as a scalar. Its maximum rate of change is in the r> direction, and its derivative in that direction is dr / dr = 1, so 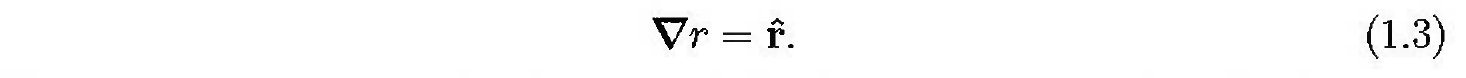 Next, we consider any scalar function,
Next, we consider any scalar function,














 Copyright Copyright 2020 by Jerrold Franklin All rights reserved. Bibliographical NoteUnderstanding Vector Calculus: Practical Development and Solved Problems is a new work, first published by Dover Publications, Inc., in 2020. International Standard Book NumberISBN-13: 978-0-486-83590-7ISBN-10: 0-486-83590-1 Manufactured in the United States by LSC Communications 83590101 www.doverpublications.com 2 4 6 8 10 9 7 5 3 1 2020 ContentsPreface My purpose in this development of vector calculus is to present it in a way that will prove useful to you for the rest of your career in science or mathematics. You can think of this presentation as a workbook for learning how to use vector calculus in practical calculations and derivations. After studying the text and doing the problems, you should not have to memorize long equations or need to look anything up while you work in your field. I want you to get to the point where you can treat the use of vector calculus on the same level as you would simple algebraic calculations, working them out as you go.
Copyright Copyright 2020 by Jerrold Franklin All rights reserved. Bibliographical NoteUnderstanding Vector Calculus: Practical Development and Solved Problems is a new work, first published by Dover Publications, Inc., in 2020. International Standard Book NumberISBN-13: 978-0-486-83590-7ISBN-10: 0-486-83590-1 Manufactured in the United States by LSC Communications 83590101 www.doverpublications.com 2 4 6 8 10 9 7 5 3 1 2020 ContentsPreface My purpose in this development of vector calculus is to present it in a way that will prove useful to you for the rest of your career in science or mathematics. You can think of this presentation as a workbook for learning how to use vector calculus in practical calculations and derivations. After studying the text and doing the problems, you should not have to memorize long equations or need to look anything up while you work in your field. I want you to get to the point where you can treat the use of vector calculus on the same level as you would simple algebraic calculations, working them out as you go.  Figure 1.1: Equipotentials i and gradients i.
Figure 1.1: Equipotentials i and gradients i. 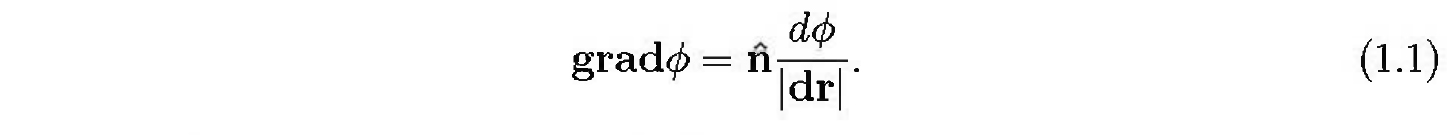 In Eq. (1.1), the unit vector
In Eq. (1.1), the unit vector 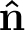 (=n/|n|) is in the direction of maximum increase of , and dr is taken in that direction of maximum increase. For infinitesimal displacements, an equipotential surface can be approximated by its tangent plane (or tangent line in two dimensions), so the change in a scalar field in an infinitesimal displacement dr will vary as the cosine of the angle between the direction of maximum gradient and dr. Then the differential change of in any direction is given by
(=n/|n|) is in the direction of maximum increase of , and dr is taken in that direction of maximum increase. For infinitesimal displacements, an equipotential surface can be approximated by its tangent plane (or tangent line in two dimensions), so the change in a scalar field in an infinitesimal displacement dr will vary as the cosine of the angle between the direction of maximum gradient and dr. Then the differential change of in any direction is given by 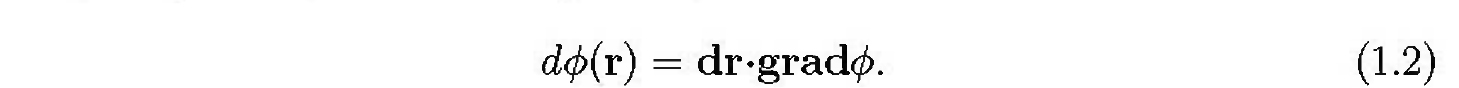 This relation can be considered an alternate definition of the gradient. The rate of change of a scalar field in a general direction a, not necessarily the direction of maximum change, can be defined by choosing dr in that direction and dividing both sides of Eq. (1.2) by the magnitude |dr|.
This relation can be considered an alternate definition of the gradient. The rate of change of a scalar field in a general direction a, not necessarily the direction of maximum change, can be defined by choosing dr in that direction and dividing both sides of Eq. (1.2) by the magnitude |dr|.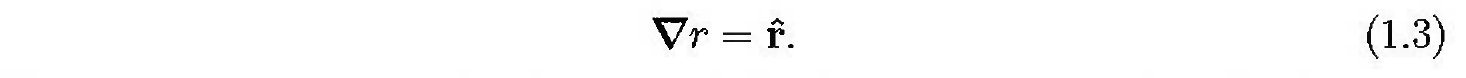 Next, we consider any scalar function,
Next, we consider any scalar function,