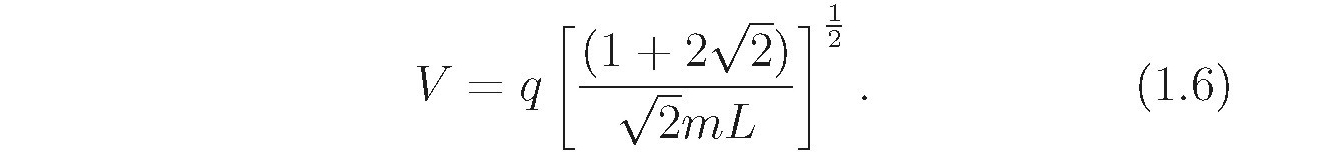Solved Problems in CLASSICAL ElectromagnetismSolved Problems in CLASSICAL ElectromagnetismJERROLD FRANKLIN Temple University DOVER PUBLICATIONS, INC. Mineola, New York Copyright Copyright 2018 by Jerrold Franklin All rights reserved. Bibliographical NoteSolved Problems in Classical Electromagnetism is a new work, first published by Dover Publications, Inc., in 2018. International Standard Book Number:ISBN-13: 978-0-486-81372-1ISBN-10: 0-486-81372-X Manufactured in the United States by LSC Communications 81372X01 2018 www.doverpublications.com Contents Preface This book of solved problems is meant to serve and help several types of students. If you are taking, or have already taken, an advanced EM course, this book is meant to be a useful adjunct to your textbook, giving you added practice in working out problems. If you have taken an undergraduate EM course, and want to prepare yourself for graduate school, I hope this book can help you achieve that aim by preparing you for the GRE, or whatever test, and getting you ready for graduate work. I also think beginners, or students not even taking a course at the moment, can get into these problems and learn just from working on them with the help of my solutions.
I think this book can be useful for students on several levels. At least, that is my intention. If you just want to develop your skills, even on your own, I believe with serious work on your part, that this book can help you in that. The book includes a number of review sections to prepare students without previous advanced training to work out the problems. I also make reference to sections of my Dover textbook, Classical Electromagnetism. Second Edition (0-486-81371-1), (referred to as [CEM]) if you want more detailed development of any topic.
Of course, you can also use any book of your choice as an additional reference. A bit of advice on how to use this book to your benefit: There are two types of problems included. Some are derivations that often will be done from a point of view you may not have seen before. You should do these problems by thinking about them, then start to do them on your own, but look over my approach before you get too bogged down. Most of the problems are real problems with calculations to work out. Work long and hard on these problems before going to my solutions.
You learn to do them on your own by doing them on your own. For these types of problems, my solutions are meant to be backups, either to look at to check your own answer or to run to if you really reach a dead end. Running to read my solutions too early will just make this a textbook instead of a workbook. There are two aspects to being a physicist: learning and doing. The learning is done in the standard course with a textbook to follow. Doing is done by doing.
That is what this book is about. One last comment, when I say Work, I dont mean you cant enjoy it. My greatest satisfaction has always been working out hard problems, even if they are done as work. The book uses Gaussian units because the problems are simpler to work out without extraneous constants. The only constant in Gaussian units is c, which was originally introduced as the ratio between emu charge and esu charge, but some time later was found to be the speed of light. In Gaussian units, electric currents or the velocity of moving charges are divided by the constant c.
Calculations are simpler in the Gaussian system because you dont have to worry about where to put  It is important to be conversant with both Gaussian units and SI units, and how to go back and forth between them. There is an appendix showing the various conversions between Gaussian quantities and the SI counterparts, but you wont need it too often to do the problems. The procedure to convert SI equations into Gaussian equations is:
It is important to be conversant with both Gaussian units and SI units, and how to go back and forth between them. There is an appendix showing the various conversions between Gaussian quantities and the SI counterparts, but you wont need it too often to do the problems. The procedure to convert SI equations into Gaussian equations is: 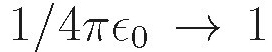 and
and 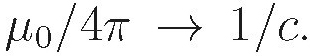 To go from Gaussian to SI:
To go from Gaussian to SI: 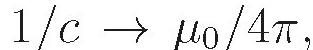 and a
and a 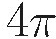 in an electricity case is usually replaced by
in an electricity case is usually replaced by 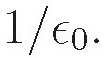 I find it easiest to convert any SI units into Gaussian to do the calculation, and then if desired, convert back to SI units for the answer. I hope you enjoy and learn from my book. Jerrold Franklin Chapter 1 Electrostatics 1.1 Static fields and forces 1.1.1 Applications of Coulombs law . ( b) Use the force in part (a) to find the velocity of one of the charges a long time after the four charges are released from rest in the original configuration. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is
I find it easiest to convert any SI units into Gaussian to do the calculation, and then if desired, convert back to SI units for the answer. I hope you enjoy and learn from my book. Jerrold Franklin Chapter 1 Electrostatics 1.1 Static fields and forces 1.1.1 Applications of Coulombs law . ( b) Use the force in part (a) to find the velocity of one of the charges a long time after the four charges are released from rest in the original configuration. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is 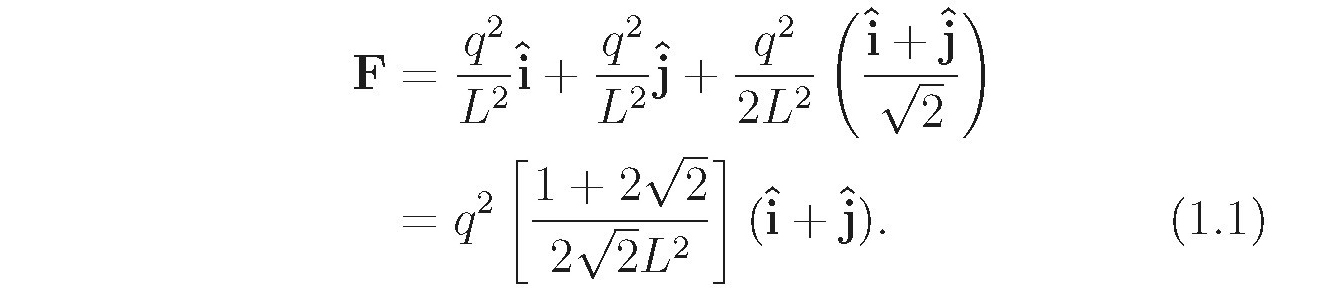 The magnitude of this force on any of the four charges is
The magnitude of this force on any of the four charges is 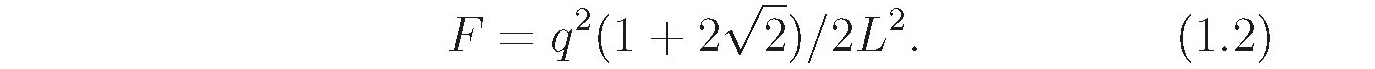 ( b) If the four charges are released from rest, we can write for the acceleration of any of the charges
( b) If the four charges are released from rest, we can write for the acceleration of any of the charges 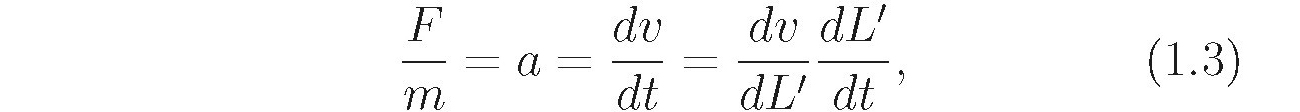 where L' is the side length of the square at any time during the motion. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is
where L' is the side length of the square at any time during the motion. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is 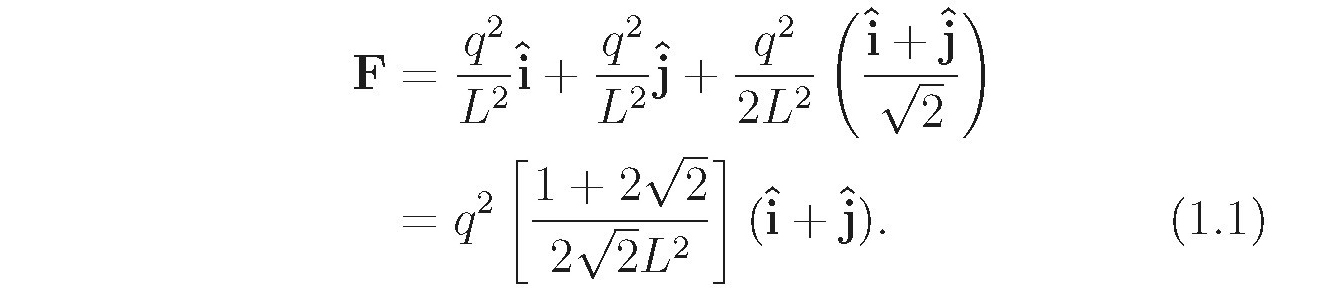 The magnitude of this force on any of the four charges is
The magnitude of this force on any of the four charges is 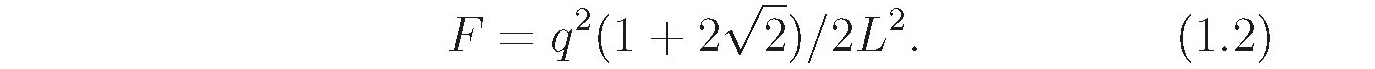 ( b) If the four charges are released from rest, we can write for the acceleration of any of the charges
( b) If the four charges are released from rest, we can write for the acceleration of any of the charges 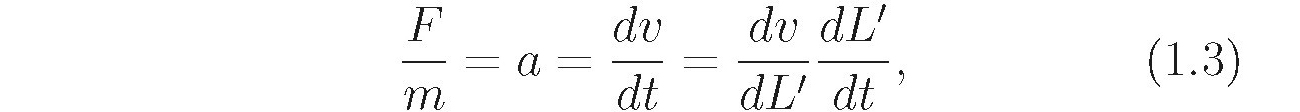 where L' is the side length of the square at any time during the motion.
where L' is the side length of the square at any time during the motion.
The center of the square remains fixed, and the distance, r, of a charge from the center is related to L' by 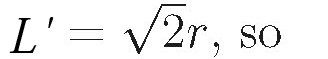
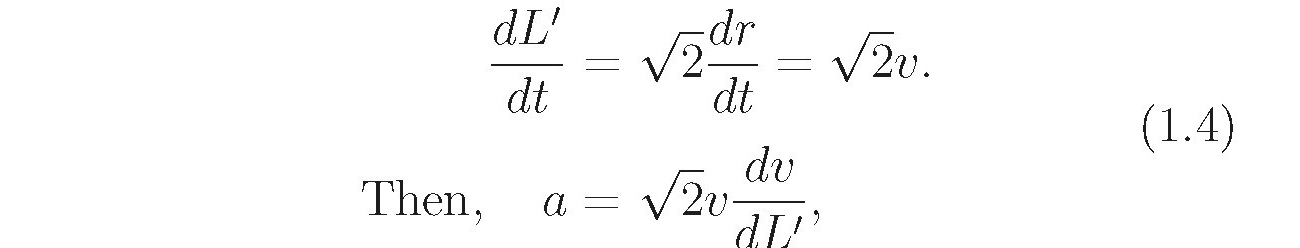 and the squared velocity after a long time is given by
and the squared velocity after a long time is given by 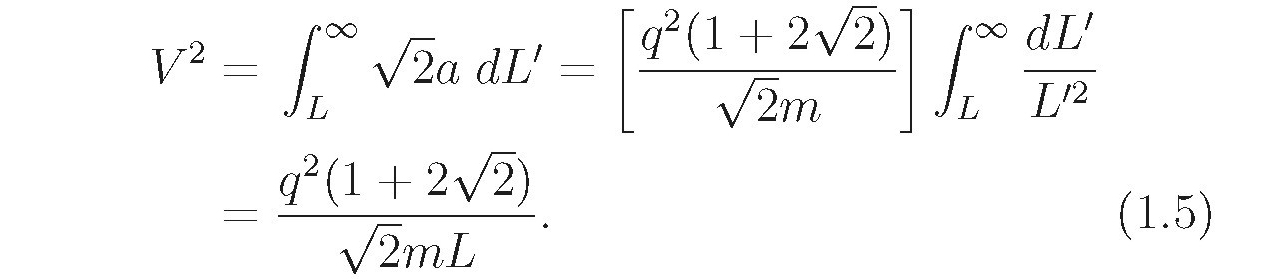 The velocity is the square root of this:
The velocity is the square root of this: 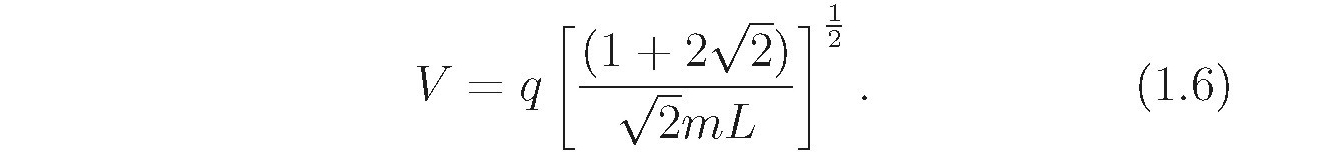
Next page












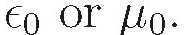 It is important to be conversant with both Gaussian units and SI units, and how to go back and forth between them. There is an appendix showing the various conversions between Gaussian quantities and the SI counterparts, but you wont need it too often to do the problems. The procedure to convert SI equations into Gaussian equations is:
It is important to be conversant with both Gaussian units and SI units, and how to go back and forth between them. There is an appendix showing the various conversions between Gaussian quantities and the SI counterparts, but you wont need it too often to do the problems. The procedure to convert SI equations into Gaussian equations is: 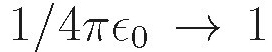 and
and 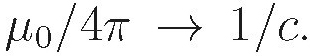 To go from Gaussian to SI:
To go from Gaussian to SI: 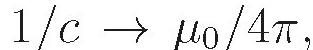 and a
and a 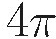 in an electricity case is usually replaced by
in an electricity case is usually replaced by 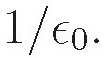 I find it easiest to convert any SI units into Gaussian to do the calculation, and then if desired, convert back to SI units for the answer. I hope you enjoy and learn from my book. Jerrold Franklin Chapter 1 Electrostatics 1.1 Static fields and forces 1.1.1 Applications of Coulombs law . ( b) Use the force in part (a) to find the velocity of one of the charges a long time after the four charges are released from rest in the original configuration. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is
I find it easiest to convert any SI units into Gaussian to do the calculation, and then if desired, convert back to SI units for the answer. I hope you enjoy and learn from my book. Jerrold Franklin Chapter 1 Electrostatics 1.1 Static fields and forces 1.1.1 Applications of Coulombs law . ( b) Use the force in part (a) to find the velocity of one of the charges a long time after the four charges are released from rest in the original configuration. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is 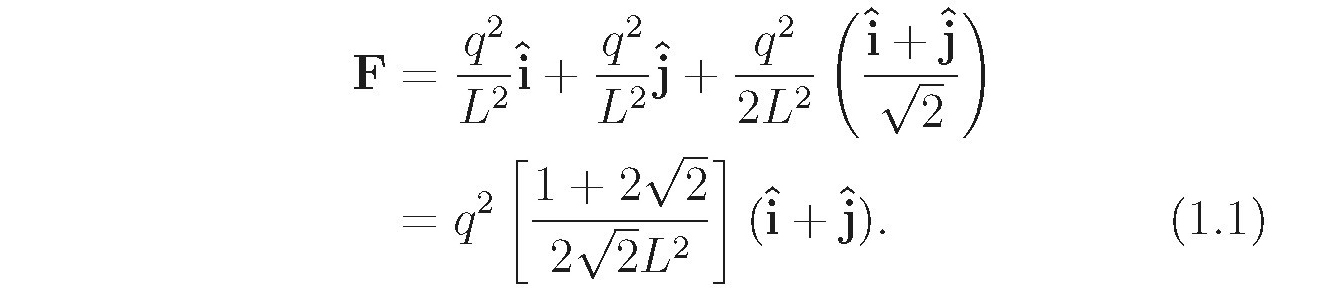 The magnitude of this force on any of the four charges is
The magnitude of this force on any of the four charges is 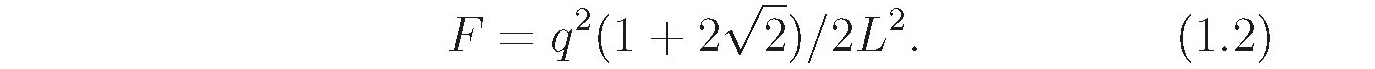 ( b) If the four charges are released from rest, we can write for the acceleration of any of the charges
( b) If the four charges are released from rest, we can write for the acceleration of any of the charges 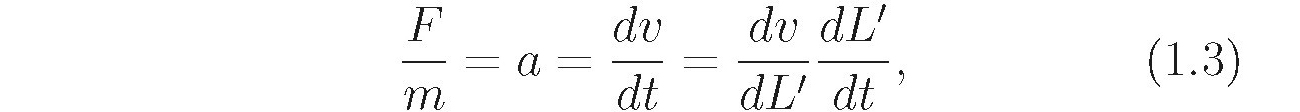 where L' is the side length of the square at any time during the motion. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is
where L' is the side length of the square at any time during the motion. Solution: ( a) The force on the upper right-hand charge due to the other three charges at the corners of a square with sides of length L is 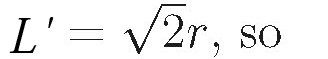
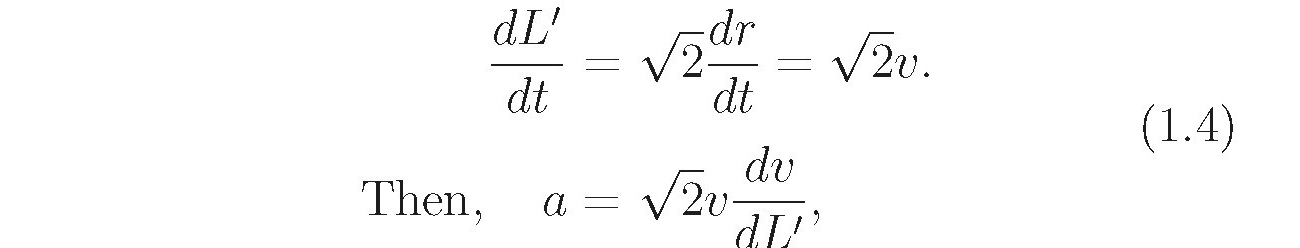 and the squared velocity after a long time is given by
and the squared velocity after a long time is given by 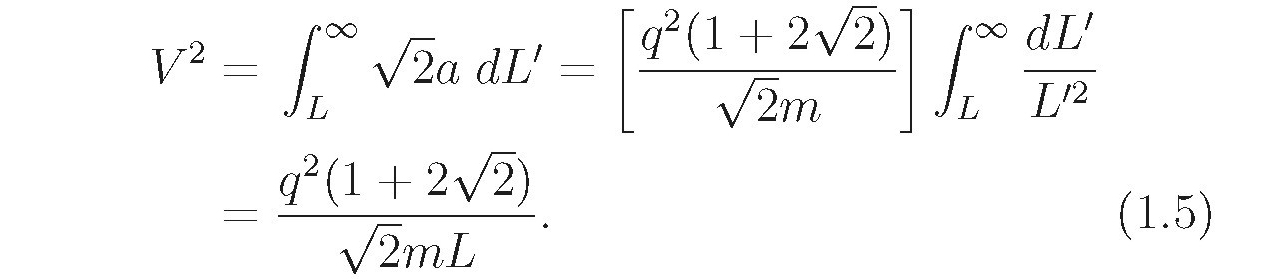 The velocity is the square root of this:
The velocity is the square root of this: