VECTOR
ANALYSIS
LOUIS BRAND DOVER PUBLICATIONS, INC.
Mineola, New York
Bibliographical Note This Dover edition, first published in 2006, is an unabridged republication of the work originally published by John Wiley & Sons, Inc., New York, in 1957.
Library of Congress Cataloging-in-Publication Data Brand, Louis, 1885 Vector analysis / Louis Brand. p. cm. Originally published: New York : Wiley, 1957. eISBN 13: 978-0-486-15484-8 1. eISBN 13: 978-0-486-15484-8 1.
Vector analysis. I. Title. QC20.7.V4B73 2006 515'.63dc22 2005049527 Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501 I dedicate this book to my former teacher and dean,
HERMAN SCHNEIDER in tribute to the originator of cooperative education at its fiftieth anniversary, 19061956: JOINING THEORY AND PRACTICE
LINKING EDUCATION AND INDUSTRY
THROUGH KNOWLEDGE AND EXPERIENCE. (Inscription at west end of the Herman Schneider Quadrangle, University of Cincinnati.)
 Preface
Preface A vectorial treatment of differential geometry, mechanics, hydrodynamics, and electrodynamics is now practically standard procedure.
The use of vectors not only simplifies and condenses the exposition but also makes mathematical and physical concepts more tangible and easy to grasp. The day is not far distant when vector algebra will be introduced in analytic geometry, thus giving the student the double advantage of an early introduction to the subject and a welcome relief from a multiplicity of formulas to be memorized. The dot and cross product of Gibbs, so intimately involved in all questions of perpendicularity and parallelism, enable one to write the equations of lines and planes at will and to solve all distance problems in the most natural manner. Even the simple distributive law, (u + v) = u + v, gives one the power to use the properties of similar triangles without figures and virtually in the dark. And then that tremendous step from two to three dimensionswhich usually occurs so late in the course that the student misses it altogetherneed never be taken at all. For we start in three dimensions, the world we actually live in, and this on the fine axiom of J.
Willard Gibbs: The whole is simpler than its parts. Vector analysis has also breached the walls of the calculus and now puts in an appearance in every modern textbook in that subject. The gradient, divergence, and rotation, in their capacity of invariants, form the natural language of spatial science. Avoidance of them is futile, and using long scalar notations every time they occur is wasteful of time and effort. I believe that the introduction of divergence and rotation from the beginning as invariants of a dyadic (the gradient of a vector) is not only the proper procedure but is actually the simplest in the long run. Although it requires a slight knowledge of dyadics, or tensors of valence two, the time is well spent; for the world is full of important tensors that the earnest student might just as well encounter head on. In this book the use of dyadics is held to a drastic minimum; and hence rigid dynamics (with its inertia dyadic) and the theory of elasticity (with its stress and strain tensors) have been regretfully omitted.
Besides, this book was designed as a short course to give a beginning student the tools of vector algebra and calculus and a brief glimpse beyond into their manifold applications. Thus the equation for the angular rate of change of a radial unit vector is actually the key to the eccentricities of gyroscopic behavior. But in this book we have stopped short of gyroscopes as being beyond its proper scope. After all, a short book in vector analysis cannot pretend to be in addition a treatise on mathematical physics. But the applications have been developed to that extent so that the uses of the potential function, both scalar and vector, are fully illustrated. Moreover the basic postulates of the sciences dealt with have been brought to the foreground to put their logical structure in sharp relief.
Since the concept of a vector has been greatly generalized in geometry and mathematical physics, the final chapter gives a brief introduction to abstract vector spaces, together with the ideas of linear dependence, basis, and dimension. As this chapter is necessarily abstract, an especial effort was made to keep the exposition as simple and clear as possible. In my more comprehensive book on Vector and Tensor Analysis, I quoted the eloquent words of Bertrand Russell on mathematics as a science and as an art. They deserve to be quoted again: The true spirit of delight, the exaltation, the sense of being more than man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as in poetry. What is best in mathematics deserves not merely to be learned as a task, but also to be assimilated as a part of daily thought, and brought again and again before the mind with ever-renewed encouragement. Real life is, to most men, a long second-best, a perpetual compromise between the real and the possible; but the world of pure reason knows no compromise, no practical limitations, no barrier to the creative activity embodying in splendid edifices the passionate aspiration after the perfect from which all great work springs.
As very full cross references are given in this book, an article as well as a page number is given at the top of each page. Equations are numbered serially are simply made by title. Bold-face type is used in the text to denote vectors or dyadics. The magnitude of a vector v is denoted by |v| or, on occasion, by . A displacement (or arrow vector) from A to B is written 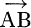 . Superimposed arrows may also be used to denote vectors in manuscript.
. Superimposed arrows may also be used to denote vectors in manuscript.
Finally, I wish to express my grateful appreciation for the contribution of the Taft fund toward typing the manuscript, and to extend thanks to my colleagues Professors Jaeger and Restemeyer for their advice and suggestions. I am also indebted to Mrs. Anne Hagedorn for her efficient and painstaking help in the preparation of the manuscript. LOUIS BRAND University of Cincinnati
January 1957 Note: A reprint edition of Louis Brands Advanced Calculus [0-486-44548-8] is available from Dover Publications, Inc. Science and the applications of science are united together as the tree and its fruit. PASTEUR VECTOR
ANALYSIS
 Chapter
ChapterVector Algebra
1.
Vectors.A vector is a directed line segment. A vector from the point A to the point B is denoted by 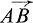 . The vector
. The vector 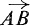 has the length AB and the direction from A to B. Besides proper vectors, which have a definite length and direction, we shall introduce the zero vector
has the length AB and the direction from A to B. Besides proper vectors, which have a definite length and direction, we shall introduce the zero vector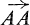 which has zero length but no definite direction. A scalar is a number whose value is the same in all systems of reference. Thus the length of a vector is a scalar; but the direction cosines of a vector are not scalars as their values depend on the choice of coordinate axes.
which has zero length but no definite direction. A scalar is a number whose value is the same in all systems of reference. Thus the length of a vector is a scalar; but the direction cosines of a vector are not scalars as their values depend on the choice of coordinate axes.












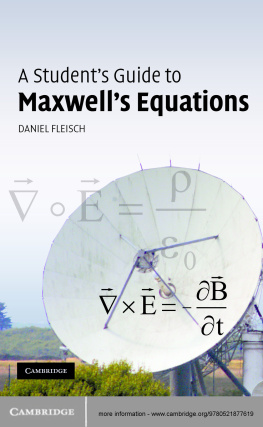




 Preface
Preface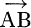 . Superimposed arrows may also be used to denote vectors in manuscript.
. Superimposed arrows may also be used to denote vectors in manuscript.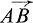 . The vector
. The vector 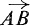 has the length AB and the direction from A to B. Besides proper vectors, which have a definite length and direction, we shall introduce the zero vector
has the length AB and the direction from A to B. Besides proper vectors, which have a definite length and direction, we shall introduce the zero vector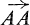 which has zero length but no definite direction. A scalar is a number whose value is the same in all systems of reference. Thus the length of a vector is a scalar; but the direction cosines of a vector are not scalars as their values depend on the choice of coordinate axes.
which has zero length but no definite direction. A scalar is a number whose value is the same in all systems of reference. Thus the length of a vector is a scalar; but the direction cosines of a vector are not scalars as their values depend on the choice of coordinate axes.