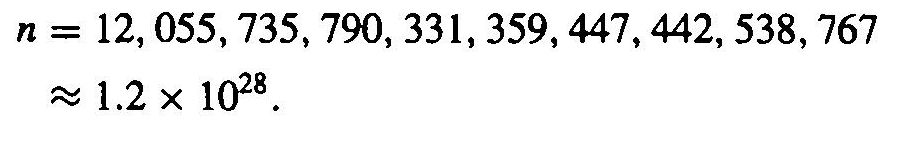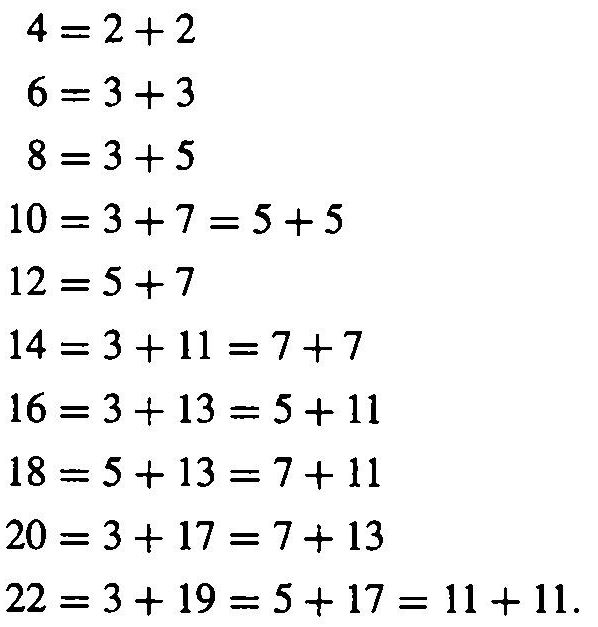Rotman - Journey into Mathematics

So, naturalists observe, a flea
Hath smaller fleas that on him prey;
And these have smaller still to bite em;
And so proceed ad infinitum.

Jonathan Swift

There are many styles of proof, and mathematical induction is one of them. We begin by saying what mathematical induction is not. In the natural sciences, inductive reasoning is based on the principle that a frequently observed phenomenon will always occur. Thus, one says that the sun will rise tomorrow morning because, from the dawn of time, the sun has risen every morning. This is not a legitimate kind of proof in mathematics, for even though a phenomenon occurs frequently, it may not occur always.

Inductive reasoning is valuable in mathematics, because seeing patterns often helps in guessing what may be true. On the other hand, inductive reasoning is not adequate for proving theorems. Before we see examples, let us make sure we agree on the meaning of some standard terms.

Definition. An integer is one of 0, 1, 1, 2, 2, 3, 3, .

Definition . An integer p 2 is called a prime number if its only positive divisors are 1 and p . An integer m 2 which is not prime is called composite .

A positive integer m is composite if it has a factorization m = ab, where a < m and b < m are positive integers; the inequalities are present to eliminate the uninteresting factorization m = m x 1. Notice that a 2: since a is a positive integer, the only other option is a = 1, which implies b = m (contradicting b < m ); similarly, b 2.

The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41. That this sequence never ends is proved in Exercise 2.10.

Consider the statement:

f ( n ) = n 2 n + 41 is a prime number for every n 1

(this is really a whole family of statements, one for each positive integer n ). As we evaluate f ( n ) for n = 1, 2, 3, 4, , 40, we obtain the following values:

It is tedious but not difficult (see Exercise 1.7) to prove that every one of these numbers is prime. Can we now conclude that all the numbers of the form f ( n ) are prime? For example, is the next number f (41) = 1681 prime? The answer is no: f (41) = 412 41 + 41 = 412, which obviously factors, and hence f (41) is not prime.

Here is a more spectacular example (which I first saw in an article by W. Sierpinski). A perfect square is an integer of the form a 2 for some positive integer a; the first few perfect squares are: 1, 4, 9, 16, 25, 36, 49. Consider the statements S( n ), one for each n 1:

S ( n ) : 991 n 2 + 1 is not a perfect square.

It turns out that many of the statements S ( n ) are true. In fact, the smallest number n for which S ( n ) is false is

The original problem is a special case of Pells equation (given a prime p, when are there integers m and n with m 2 = pn 2 + 1), and there is a way of calculating all possible solutions of it. In fact, an even more spectacular example of Pells equation involves the prime p = 1, 000, 099; the smallest n for which 1, 000, 099 n 2 + 1 is a perfect square has 1116 digits.) The latest scientific estimate of the age of the earth is 20 billion (20,000,000,000) years, or about 7.3 1012 days, a number very much smaller than 1.2 1028, let alone 101115. If, starting on the very first day, mankind had verified statement S ( n ) on the nth day, then there would be, today, as much evidence of the general truth of these statements as there is that the sun will rise tomorrow morning. And yet some statements S ( n ) are false!

As a final example, let us consider the following statement, known as Goldbachs Conjecture: Every even number m 4 is a sum of two primes. For example,

It would be foolish to demand that all odd numbers be sums of two primes. For example, suppose that 27 = p + q, where p and q are primes. If both p and q are odd, then their sum is even, contradicting 27 being odd. Since the only even prime is 2, we have 27 = 2 + q, and so q = 25 is prime; this contradiction shows that 27 is not a sum of two primes.

No one has ever found a counterexample to Goldbachs conjecture, but neither has anyone ever proved it. At present, the conjecture has been verified for all even numbers m 1013 by H. J. J. te Riele and J.-M. Deshouillers. It has been proved by J.-R. Chen (with a simplification by P. M. Ross) that every sufficiently large even number m can be written as p + q, where p is prime and q is almost a prime; that is, q is either prime or a product of two primes. Even with all this positive evidence, however, no mathematician will say that Goldbachs conjecture must, therefore, be true for all even m.

We have seen what mathematical induction is not; let us now discuss what induction is. Suppose one guesses that all the statements S ( n ) of a certain sort are true (for example, suppose that S( n ) has been observed to be true for many values of n ). Induction is a technique of proving that all the statements S ( n ) are, indeed, true. For example, the reader may check that n > n for many values of n, but is this inequality true for every value of n ? We will prove below, using induction, that this is so.