A. J. M. Spencer - Continuum Mechanics
Here you can read online A. J. M. Spencer - Continuum Mechanics full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2004, publisher: Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Continuum Mechanics
- Author:
- Publisher:Dover Publications
- Genre:
- Year:2004
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Continuum Mechanics: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Continuum Mechanics" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
The mechanics of fluids and the mechanics of solids represent the two major areas of physics and applied mathematics that meet in continuum mechanics, a field that forms the foundation of civil and mechanical engineering. This unified approach to the teaching of fluid and solid mechanics focuses on the general mechanical principles that apply to all materials. Students who have familiarized themselves with the basic principles can go on to specialize in any of the different branches of continuum mechanics. This text opens with introductory chapters on matrix algebra, vectors and Cartesian tensors, and an analysis of deformation and stress. Succeeding chapters examine the mathematical statements of the laws of conservation of mass, momentum, and energy as well as the formulation of the mechanical constitutive equations for various classes of fluids and solids. In addition to many worked examples, this volume features a graded selection of problems (with answers, where appropriate). Geared toward undergraduate students of applied mathematics, it will also prove valuable to physicists and engineers.
A. J. M. Spencer: author's other books
Who wrote Continuum Mechanics? Find out the surname, the name of the author of the book and a list of all author's works by series.












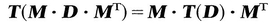
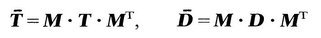
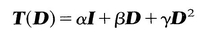
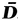 , tr D 2 = tr
, tr D 2 = tr 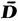 2, and tr D 3 = tr
2, and tr D 3 = tr 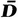 3. Hence , and are unchanged if D ij are replaced by
3. Hence , and are unchanged if D ij are replaced by 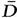 ij.
ij.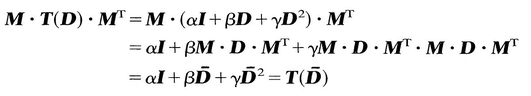
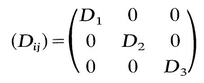
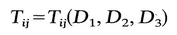
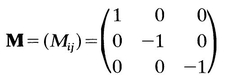
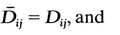
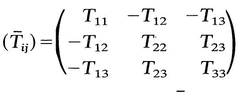
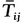 = T ij. Hence T 12 = 0, T 13 = 0. Similarly, by another choice of M , it can be shown that T 23=0. Thus if (D j ) is a diagonal matrix, so is ( T ij); that is, D and T have the same principal axes. Therefore we can now write
= T ij. Hence T 12 = 0, T 13 = 0. Similarly, by another choice of M , it can be shown that T 23=0. Thus if (D j ) is a diagonal matrix, so is ( T ij); that is, D and T have the same principal axes. Therefore we can now write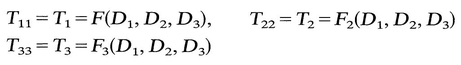
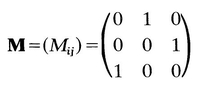
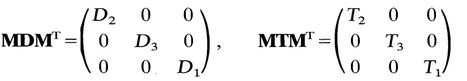
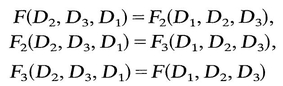
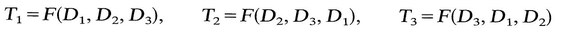
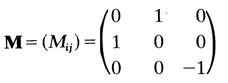
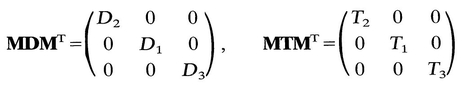
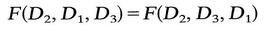
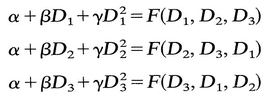
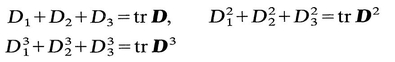
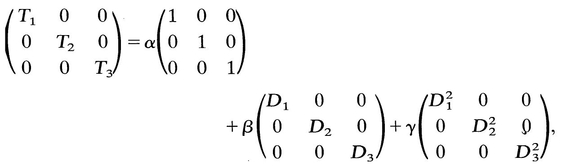
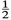 sin 2) = 2 Ua 2( z z 0) where x 1 = r cos , x 2 = r sin
sin 2) = 2 Ua 2( z z 0) where x 1 = r cos , x 2 = r sin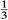 A
A 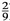 )eA (b) f = 2 e 112 e 2 + 6 e 3
)eA (b) f = 2 e 112 e 2 + 6 e 3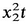 : x 2 x 3 t . Hence d x 2/d x 3 = x 2/ x 3
: x 2 x 3 t . Hence d x 2/d x 3 = x 2/ x 3