Chadwick - Continuum mechanics: concise theory and problems
Here you can read online Chadwick - Continuum mechanics: concise theory and problems full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Mineola;N.Y, year: 1999;2016, publisher: Dover Publications, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Continuum mechanics: concise theory and problems
- Author:
- Publisher:Dover Publications
- Genre:
- Year:1999;2016
- City:Mineola;N.Y
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
- 60
- 1
- 2
- 3
- 4
- 5
Continuum mechanics: concise theory and problems: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Continuum mechanics: concise theory and problems" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Continuum mechanics: concise theory and problems — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Continuum mechanics: concise theory and problems" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
CONTINUUM MECHANICS
Concise Theory and Problems
Second Corrected and Enlarged Edition
P. CHADWICK
School of Mathematics and Physics University of East Anglia, Norwich
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 1976 by George Allen & Unwin, Ltd.
New material copyright 1999 by P. Chadwick
All rights reserved.
Bibliographical Note
This Dover edition, first published in 1999, is a corrected and enlarged edition of the work originally published in 1976 by George Allen & Unwin Ltd., London. It contains four new appendices written by the author especially for the Dover edition.
Library of Congress Cataloging-in-Publication Data
Chadwick, Peter, 1931
Continuum mechanics : concise theory and problems / P. Chadwick. 2nd corr. and enl. ed.
p. cm.
Corrected and enlarged ed. of the work originally published in 1976 by George Allen & Unwin, Ltd., London.
Includes index.
ISBN-13: 978-0-486-40180-5 (pbk.)
ISBN-10: 0-486-40180-4 (pbk.)
1. Continuum mechanics. I. Title.
QA808.C46 1999
531dc21
99-38303
CIP
Manufactured in the United States by Courier Corporation
40180405
www.doverpublications.com
CONTINUUM MECHANICS
Concise Theory and Problems
Preface
At the present time the number of universities and colleges offering courses on continuum mechanics is increasing and the advantages of presenting to students a unified basis for further work in fluid dynamics and the mechanics of solid materials are being more widely recognized by teachers of theoretical mechanics. A subject which is relatively new to degree syllabuses inevitably takes some time to receive adequate textbook coverage, and exercises suitable for use in class and in set work are apt initially to be in short supply. This book is an outgrowth of lecture courses which have been given over the past six years in the University of East Anglia to second- and final-year undergraduates specializing in mathematics and to first-year graduate students taking a masters degree course in theoretical mechanics. Colleagues engaged in the teaching of continuum mechanics have urged me to give wider currency to the sets of problems which have been compiled for use in tutorials and examples classes and in the examinations associated with these courses. This material appears here in an expanded form, and in view of the lack of suitable elementary textbooks to which readers can be referred for accounts of the underlying results, an explanatory text has been provided.
The book is intended primarily for use in conjunction with a lecture course, or equivalent form of teaching. The treatment of the principles of continuum mechanics, while reasonably complete mathematically, is, by design, concise; and to a considerable extent physical considerations, motivating arguments and detailed interpretations have been omitted. In matters of this kind the individual teacher will wish to exercise his own point of view: if the time at his disposal is increased by the availability to his students of this plain account of the theoretical groundwork, I shall be well satisfied. The emphasis throughout is on the mechanics of continuous media in general, and the book ends at a point from which courses specifically devoted to the mechanics of fluids and solid materials could logically proceed. Illustrative problems on linearly viscous fluids and isotropic elastic solids are given in the last two sections in order to provide links with traditional developments of these subjects.
The reader is assumed to have a knowledge of algebra and analysis which includes the theory of vector spaces and calculus in n-dimensional Euclidean space, and familiarity with particle and rigid body mechanics and the geometrical treatment of vectors is taken for granted. In Britain a student reading for honours in mathematics normally covers these topics in the first half of his course, while most students reading mathematical or theoretical physics, or taking a combined honours course, should be adequately prepared by the start of the final year. For applied science students the subject-matter is likely to be accessible only at post-graduate level.
In a book catering mainly for the needs of beginners in continuum mechanics I have not felt it appropriate to give references to the original sources of all the material presented. An advanced treatment of the matters discussed in these pages, with full historical notes and literature references, can be found in the authoritative works of Truesdell-Toupin and Truesdell-Noll, and I wish to acknowledge here my indebtedness to the writings of these authors.
I shall be grateful for any suggestions or corrections from those who use this book.
P.C.
C Truesdell and R. A. Toupin, The Classical Field Theories. Handbuch der Physik (ed. S. Flgge) Vol. III/1, pp. 226858 (Berlin etc., Springer, 1960).
C. Truesdell and W. Noll, The Non-Linear Field Theories of Mechanics. Handbuch der Physik (ed. S. Flgge) Vol. III/3 (Berlin etc., Springer, 1965).
Contents
Note to the reader
In each chapter equations to which subsequent reference is made are numbered from . The same convention applies in references to sections, problems, exercises and figures.
Chapter 1
VECTOR AND TENSOR THEORY
The theory of scalar-, vector- and tensor-valued functions defined on subsets of a three-dimensional Euclidean space is a major part of the mathematical framework upon which continuum mechanics is built. This chapter is intended to provide a concise survey of basic results needed in the rest of the book and its contents will be found to be closely integrated into the subsequent text. It is not advisable, however, for the reader to postpone his study of continuum mechanics until the whole of this material has been mastered. Rather he should use to refresh, and perhaps reorientate, his knowledge of vector algebra and analysis, and then turn back to the topics discussed in the remaining sections as the need arises.
1VECTOR ALGEBRA
The scalar and vector products, with which the reader is already assumed to be familiar, can be defined by a system of axioms and we follow this approach here as a means of reviewing briefly the essential facts of vector algebra and, at the same time, providing a natural starting point for the development of tensor algebra. Contact with the geometrical viewpoint customarily adopted in elementary treatments of vector theory is made in .
Let  be a three-dimensional vector space over the field
be a three-dimensional vector space over the field  of real numbers. We say that
of real numbers. We say that  is a Euclidean vector space if, to each pair of vectors a, b in
is a Euclidean vector space if, to each pair of vectors a, b in 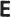 , there corresponds a scalar (in
, there corresponds a scalar (in  ), denoted by a . b and called the scalar product of a and b, and a vector (in
), denoted by a . b and called the scalar product of a and b, and a vector (in 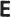 ), written ab and referred to as the vector product of a and b, with the following properties:
), written ab and referred to as the vector product of a and b, with the following properties:

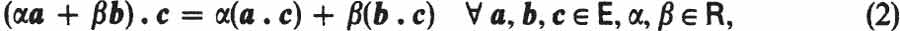
Font size:
Interval:
Bookmark:
Similar books «Continuum mechanics: concise theory and problems»
Look at similar books to Continuum mechanics: concise theory and problems. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Continuum mechanics: concise theory and problems and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.