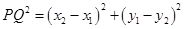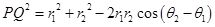CHAPTER1: CO-ORDINATES AND VECTORS
1: Coordinates of a point.
ReneDes Cartes , an ailing boy, developed Coordinate Geometry while lyingconfined to bed and watching a spider moving about its cobweb to catch itstrapped prey. Although , according to some, Fermat had proved many results ofCoordinate Geometry earlier , the time was that of a great social turbulenceknown as the renaissance period in the History of France or the Frenchrevolution and Des Cartes came to be known as the inventor of CoordinateGeometry. However, details of History is not our point and we should haveenough respect for either of them.
Inthe plane of the paper we fix a point for reference O, called the origin ofcoordinates and two intersecting straight lines XOX and YOY intersecting at Oat right angles. Such a system of reference is called a rectangularCartesian system of coordinates.( If the angle between them is not a right angle, the system is calledoblique Cartesian coordinate system. Majority of results of rectangular systemalso hold good in oblique coordinate system with suitable modifications.) If a particular point P in this planeis reached by going through a distance a from the origin towards X-direction(towards the right) from the origin O and then going through a distance b inY-direction (upwards from there), then the coordinates of the point P withreference to the set axes and origin are denoted by the ordered pair (a, b) andb are called x-coordinate (called the abscissa) and y-coordinate(called the ordinate) of the point P. The point P is written as P(a, b).Thepoint is unique if and b are given numbers. and b are lengths of perpendicularsfrom the point on the x-axis and y-axis respectively.
2: Coordinate Geometry in threedimensions:
Apoint in three dimensional space can be represented by an ordered triplet (a,b, c) where a, b and c are lengths of perpendiculars from the point on the yzplane, xz plane and xy plane respectively. The point can be reached byproceeding through a distance a (= OR) from the origin O of reference systemalong the rectangular Cartesian coordinate x-axis in the direction of X, thenthrough a distance b (= RQ) in the direction of Y, parallel to Y-axis and thenthrough a distance c (= QP) in direction of Z parallel to Z axis where thethree axes perpendicular to each other meeting at O. The convention is that theaxes are mutually perpendicular in the sense that, if fingers of right handpoint straight in the direction of X, then turned towards the direction of Ymaking a fist, then the thumb pointing upwards from the fist should be in thedirection of Z.
In contrastwith two dimensional Coordinate Geometry, if perpendiculars are dropped fromthe point on the axes of X, Y an Z their lengths are not the lengths of thecoordinates ! (verify from the figure 1.5a that PT, the perpendicular from thepoint on z-axis = OQ = (OR2+RQ2) = (x2+y2) z). Actually, the perpendicular from the point on xy-plane, is the z-coordinateif this plane passes through the origin. Similar statement may be made for xand y coordinates.
But thedistance of the point from the origin OP = (PQ2+OQ2)= (PQ2+OR2+RQ2)
= (x2+y2+z2),similar formula as in two dimensions.
3: Distance between two points:In two dimensions
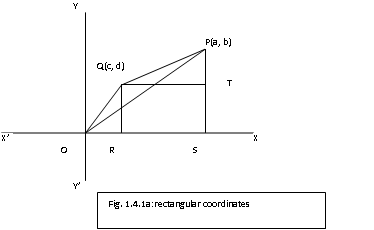
Inthe figure above, in a typical rectangular Cartesian coordinate systemtwo points P(a, b) and Q(c, d) are shown joined to each other and to the OriginO.
a = OS, b =PS, c = OR , d = QR = TS. The moduli (plural of modulus) of P and Q are
OP = (a2 +b2 ), OQ = ( c2+d2 ),
Thedistance PQ =(( a c)2 +(b d)2 ).
4: Distance between two points:In three dimensions:
Let P(x1,y1, z1) and Q(x2, y2, z2) are any two points with coordinates (x1, y1, z1)and
(x2, y2,z2) respectively as in fig. Fig.1.5b . Drop perpendiculars PTand QS on the
xy-plane and let PR be the perpendicular on QS. Drop perpendiculars TU and SV on the x-axisand let UW be the perpendicular on SV.
We have RS =PT= z1, QR = QS SR = QS PT = z2 z1 and PR =TS
= {(x2 x1)2+(y2 y1)2} as intwo dimensions.
So PQ2= PR2 + RQ2 = TS2+RQ2 = [ {(x2 x1)2+(y2 y1)2}]2+(z2 z1)2
Or, (x2 x1)2+(y2 y1)2+(z2 z1)2
So thedistance = {(x2 x1)2+(y2 y1)2+ (z2 z1)2}.
5: Polar Coordinates :
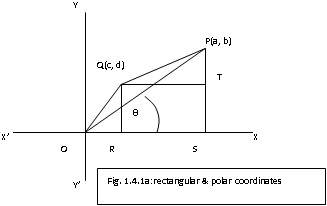
Inthe same figure, instead of the X and Y axes of coordinates, if we keep thefixed point O (called the pole) and the fixed line OX, called theinitial line, we can reach the points P by advancing through a distance r fromO in X direction, and then turning through an angle q anticlockwise = angle XOP. Thus the point P is uniquely determined here alsowith polar coordinates, (r , q ) , the system of coordinates beingcalled polar coordinate system. In this system the line OX is called theinitial line and the angle is called the vectorial angle.
If(x , y) be the coordinates of some point in rectangular system and (r , q )be the coordinates of the same point in polar system, we can easily change thesystem of coordinates from one to the other easily.
Younever need cramming the equations in the study of Calculus, nor the processwhich generated it. It is just needed to understand that a curve is thelocus or path of a point changing according to a given equation andis completely described by the equation involving the coordinates x and y,which is arrived by applying the criteria describing the curve..
6: Change of Coordinates fromCartesian to polar or vice versa:
There isnothing holy about Cartesian coordinates or polar coordinates or any particularsystem of coordinates in particular. One can easily note the relations
r = (x2+ y2) and tan q = y / x
or q = tan -1 (y / x)
to replace (x,y) with (r, q ) . Or the relations
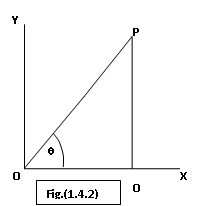
x= r cos q , and y = r sin q as would be evident from theFig.(1.4.2).
Thus (r, q )can be replaced by (x, y)
(For any pointP(x, y), x =OQ = r cos q , and y = PQ = r sin q where OP = r and angle POQ = q and as such the above relations areevident .)
7: Distance between two points in polar coordinates:
Supposethe two points are 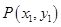 and
and 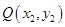 respectively.By changing to polar coordinates,
respectively.By changing to polar coordinates, 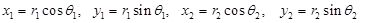 . Then,
. Then,
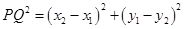

Onsimplification this gives, 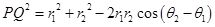
Directapplication of cosine formula from trigonometry also could have given thisresult. Join P, Q to the origin O and apply cosine formula to OPQ toget PQ.
Next page













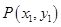 and
and 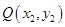 respectively.By changing to polar coordinates,
respectively.By changing to polar coordinates, 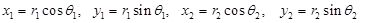 . Then,
. Then,