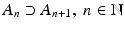Cannarsa Piermarco - Introduction to Measure Theory and Functional Analysis
Here you can read online Cannarsa Piermarco - Introduction to Measure Theory and Functional Analysis full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, year: 2015, publisher: Springer International Publishing, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Introduction to Measure Theory and Functional Analysis
- Author:
- Publisher:Springer International Publishing
- Genre:
- Year:2015
- City:Cham
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Introduction to Measure Theory and Functional Analysis: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Introduction to Measure Theory and Functional Analysis" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Cannarsa Piermarco: author's other books
Who wrote Introduction to Measure Theory and Functional Analysis? Find out the surname, the name of the author of the book and a list of all author's works by series.





![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)







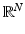 . Starting from such an intuitive idea, by a covering process one can assign to any set a nonnegative number which quantifies its extent. Such an association leads to the introduction of a set function called exterior measure , which is defined for all subsets of
. Starting from such an intuitive idea, by a covering process one can assign to any set a nonnegative number which quantifies its extent. Such an association leads to the introduction of a set function called exterior measure , which is defined for all subsets of 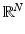 . The exterior measure is monotone but fails to be additive. Following Carathodorys construction, it is possible to select a family of sets for which the exterior measure enjoys further properties such as countable additivity. By restricting the exterior measure to such a family one obtains a complete measure . This is the procedure that allows to define the Lebesgue measure in
. The exterior measure is monotone but fails to be additive. Following Carathodorys construction, it is possible to select a family of sets for which the exterior measure enjoys further properties such as countable additivity. By restricting the exterior measure to such a family one obtains a complete measure . This is the procedure that allows to define the Lebesgue measure in 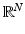 . The family of all Lebesgue measurable sets is very large: sets that fail to be measurable can only be constructed by using the Axiom of Choice.
. The family of all Lebesgue measurable sets is very large: sets that fail to be measurable can only be constructed by using the Axiom of Choice.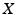 . In the particular case of
. In the particular case of 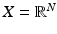 , a special role is played by Radon measures (of which the Lebesgue measure is an example) that have important regularity properties.
, a special role is played by Radon measures (of which the Lebesgue measure is an example) that have important regularity properties. -Algebras of Sets
-Algebras of Sets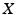 a nonempty set, by
a nonempty set, by 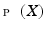 the set of all parts (i.e., subsets) of
the set of all parts (i.e., subsets) of 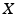 , and by
, and by 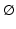 the empty set.
the empty set.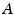 of
of 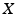 we shall denote by
we shall denote by 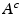 its complement, i.e.,
its complement, i.e., 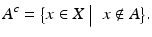
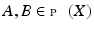 we set
we set 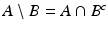 .
.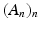 be a sequence in
be a sequence in  . The following De Morgan identity holds:
. The following De Morgan identity holds: 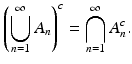
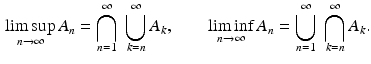
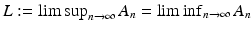 , then we set
, then we set 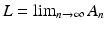 , and we say that
, and we say that 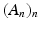 converges to
converges to 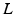 (in this sense we shall write
(in this sense we shall write 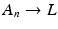 ).
).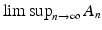 (resp.,
(resp., 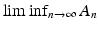 ) consists of those elements of
) consists of those elements of 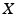 that belong to infinitely many subsets
that belong to infinitely many subsets 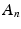 (resp., that belong to all but a finite number of subsets
(resp., that belong to all but a finite number of subsets 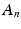 ). Therefore
). Therefore 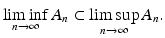
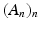 is increasing (
is increasing ( 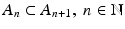 ), then
), then 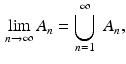
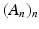 is decreasing (
is decreasing (