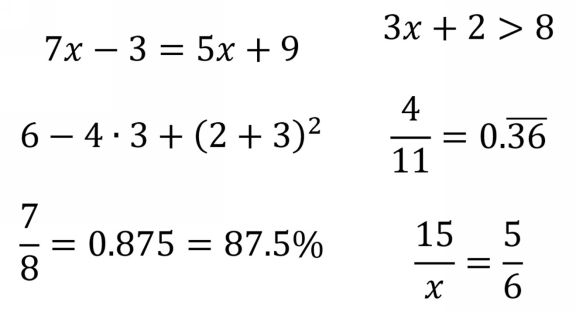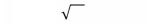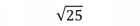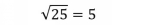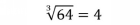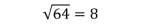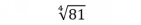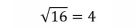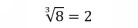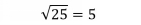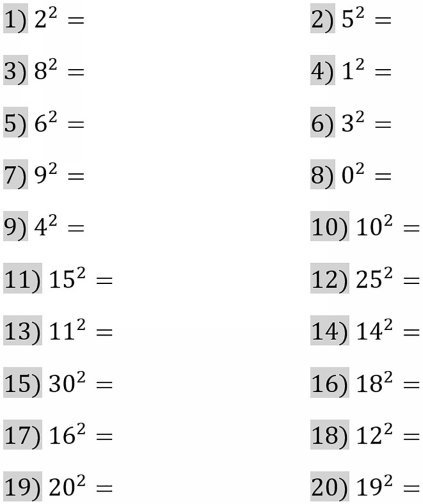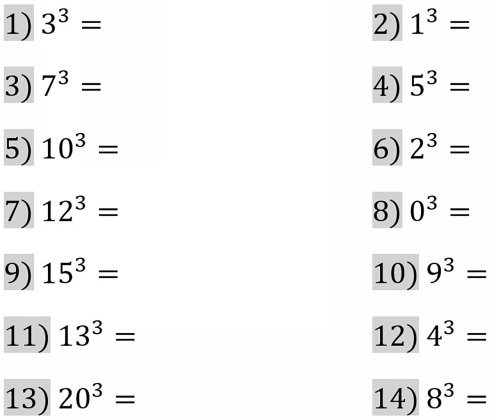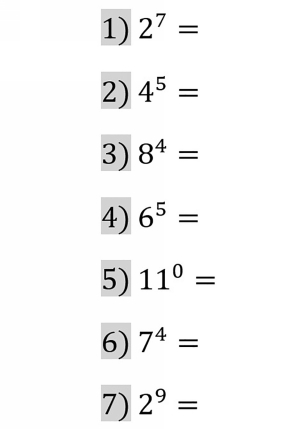Chris McMullen - Essential Prealgebra Skills Practice Workbook

Essential

PREALGEBRA

Skills Practice Workbook

Chris McMullen, Ph.D.

COPYRIGHT

Essential Prealgebra Skills Practice Workbook

Chris McMullen, Ph.D.

Copyright 2020 Chris McMullen, Ph.D.

monkeyphysicsblog.wordpress.com

improveyourmathfluency.com

chrismcmullen.com

All rights are reserved. However, teachers or parents who purchase one copy of this workbook (or borrow one physical copy from a library) may make and distribute photocopies of selected pages for instructional (non-commercial) purposes for their own students or children only.

Zishka Publishing

Paperback Edition ISBN: 978-1-941691-08-3

Mathematics > Arithmetic

Mathematics > Algebra > Beginning

CONTENTS

INTRODUCTION

The goal of this workbook is to help prepare students for a successful transition from arithmetic to algebra. Following is a sample of what to expect:

Improve arithmetic fluency. Since arithmetic is used to solve algebra problems, it is important for students to be fluent in their arithmetic skills. The exercises in this workbook involve a variety of arithmetic skills to help build fluency.

Fractions, decimals, and percents. Fractions come about naturally when doing algebra. This workbook has separate chapters devoted to fractions, decimals, and percents.

Build a strong foundation. Fundamental algebra concepts such as combining like terms, isolating the unknown, and factoring are introduced. Developing a solid foundation is essential toward mastering the subject of algebra.

Beginning algebra practice. Chapters 6-7 focus on simplifying basic expressions and solving simple equations. This lets students learn to swim in the shallow end before diving into the deep end.

Thinking through math. Students who succeed at higher levels of mathematics learn to think their way through the math. Strive to get your students to think through the exercises. Students who try to understand the ideas and the logic behind the examples are more likely to be successful.

Answer key. Practice makes permanent, but not necessarily perfect. Check the answers at the back of the book and strive to learn from any mistakes. This will help to ensure that practice makes perfect.

1 ARITHMETIC OPERATIONS

An exponent appears to the top right of a number, like the 2 in 4 or the 5 in 3 . An exponent is basically shorthand for repeated multiplication, as shown by the examples below.

= 4 4

= 2 2 2

= 7 7 7 7

= 3 3 3 3 3

As shown above, an exponent tells you how many times to multiply a number by itself. For example, 10 means to have 6 tens multiplying each other:

= 10 10 10 10 10 10

A power is another term for exponent. In 8 , we may call 3 the exponent or we may call it the power, whereas 8 is called the base .

When the power equals 2, we call it a square . For example, 6 reads as 6 squared.

When the power equals 3, we call it a cube . For example, 8 reads as 8 cubed.

The symbol

is called the radical sign . It is used to indicate a root.

A square root asks, Which number multiplied by itself equals the value under the radical? For example,

asks, What number times itself equals 25? One answer is

since 5 5 = 25.

A cube root asks, Which number cubed equals the value under the radical? We write a small 3 to the left of the radical sign to indicate a cube root. For example,

is the cube root of 64 since 4 = 4 4 4 = 64. In contrast,

is the square root of 64.

Other roots can be similarly indicated. For example,

is the fourth root of 81. The answer to

is 3 because 3 = 3 3 3 3 = 81.

A square root is basically the opposite of a square. For example, compare 4 = 4 4 = 16 to

Similarly, a cube root is basically the opposite of a cube. For example, compare 2 = 2 2 2 = 8 to

What happens if the power is 0 or 1, like 5 or 9 ? Good question. See Sec. 1.3.

Do exponents really save that much time? You bet. Try writing 3 the long way.

Why does it say, One answer is

Is that because there is another answer? Yes! See Sec. 1.6.

Can you have a negative power, like 2 ? Yes, you can. See Sec. 1.5.

Can you have fractional powers, like 8 2/3 ? Yes! See Chapter 3.

1.1 Squares

To square a number, multiply the number by itself.

Example 1 . 7 = 7 7 = 49

Example 2 . 13 = 13 13 = 169

1.2 Cubes

To cube a number, multiply the number by itself two times.

Example 1 . 6 = 6 6 6 = 36 6 = 216

Example 2 . 11 = 11 11 11 = 121 11 = 1331

1.3 Powers

The power tells you how many times to multiply a number by itself. Follow the examples.

Example 1 . 5 = 5 5 5 5 = 25 25 = 625

Example 2 . 3 = 3 3 3 3 3 3 = 9 9 9 = 81 9 = 729

Example 3 . 2 = 2 2 2 2 2 = 4 4 2 = 16 2 = 32

What about a power of one? Thats easy: 7 = 7. Here, there is just one 7.

What about a power of zero? Thats also easy, but trickier to understand: 10 = 1. Why does 10 = 1? Consider that 10 = 100, 10 = 1000, 10 = 10,000, 10 = 100,000, etc. Note that 10 m n = 10 m+n . (You can verify this rule for any values of m and n. Try it! For example, 10 = 100 1000 = 100,000 = 10 .) If you plug m = 2 and n = 0 into the formula, youll get 10 = 10 , which becomes 100 10 = 100. In order for 100 10 = 100 to be true, we need 10 = 1. This is one way to see that raising any nonzero number to the power of zero is equal to one. For example, 3 = 1.