Erin Highling - Take Me Out to the Math Game: Home Run Activities, Big League Word Problems and Hard Ball Quizzes—A Fun Workbook for 4-6th Graders

Text copyright 2018 Erin Highling. Design and concept copyright 2018 Ulysses Press and its licensors. All rights reserved. Any unauthorized duplication in whole or in part or dissemination of this edition by any means (including but not limited to photocopying, electronic devices, digital versions, and the internet) will be prosecuted to the fullest extent of the law. Published in the United States by: Ulysses Press P.O. Box 3440 Berkeley, CA 94703 www.ulyssespress.com ISBN: 978-1-61243-810-8 Acquisitions editor: Casie Vogel Managing editor: Claire Chun Editor: Shayna Keyles Proofreaders: Renee Rutledge Front cover design: Rebecca Lown Cover art: bats and ball augustos/shutterstock.com; baseball player omnimoney/shutterstock.com Interior design: Jake Flaherty CONTENTS Table of Contents This workbook is a fun and engaging way to practice your math skills by relating every problem to baseball.

Each activity in the book is based on real baseball situations, like batting averages, pitching speed, and even stadium size. Use these scenarios to improve your math skills while also learning more about the game of baseball, on and off the field. Each chapter focuses on a different math skill. You can go straight through the book, practicing each skill, or you can go to a specific chapter you need more practice with. There are two types of activities in this book: Game-Day Situations are real-world word problems based on baseball scenarios, and Batting Practice are practice problems to help you perfect a math skill. If you ever need any help, ask a parent or teacher to look at the Coaching pages in the back of the book to give you a hand.

Make it to the pros by completing all of the problems in Game-Day Situations or simply choose the problems that you feel best suits your abilities. There are standard problems, marked with a single baseball; challenge problems, marked with a double baseball; and super-challenge problems, marked with a triple. They look like this: Standard Problems Challenge Problems Super-Challenge Problems How to Be a Real-World Problem Solver Mathematicians need their very own set of guidelines for how they solve problems in the real world, just like baseball players do. A mathematician and a baseball player both have to use strategy, make models, notice patterns, and persevere. Lets take a closer look at these processes or skills needed to solve real-world mathematical situations every day. 1) Make sense of problems and persevere in solving them.

Read, take notice, and build understanding of the situations. Persevere when problems are challenging. Before solving a real-world math problem, take the situation apart step by step and analyze what is happening. Then, try to solve the problem with any strategy that comes to mind. If it fails, thats OK; failing and trying again means the brain is growing. You must not give up, even if you continue to fail.

Keep trying different methods to solve the problem. 2) Reason abstractly and quantitatively. Write number sentences to describe numbers and symbols within situations Use numbers or symbols to represent situations When solving problems, its important to think about the relationships between numbers and situations. You must take a situation and find a way to represent it using a number sentence or pictures. Then, manipulate it in a way that makes sense to you. 3) Construct viable arguments and critique the reasoning of others. 3) Construct viable arguments and critique the reasoning of others.

Explain your thinking using numbers, words, and/or models. Listen and ask questions to understand the thinking of others. Explain your thinking using objects, numbers, drawings, or diagrams. Solutions should be reasonable and based on the situation. When working with others, you should listen to their ideas, ask questions, analyze how their solutions are similar or different from yours, and whether those solutions make sense to the situation. 4) Model with mathematics.

Use visual models to solve problems. Real-world problem solvers use number sentences, diagrams, graphs, flowcharts, or formulas to solve problems. You should constantly ask yourself, Do these models match the context of the situation? Does this make sense? And if it doesnt, be willing to go back and re-evaluate your model. 5) Use tools strategically. Choose and use math tools that are appropriate to the problems. 6) Attend to precision. 6) Attend to precision.

Work accurately and communicate clearly. Discuss the mathematical situation and solution with others in a detailed way, using clear definitions and explanations of symbols, diagrams, and/or number sentences. Use the most efficient strategies when solving problems in order to come to the most precise and accurate calculations. Be sure that all word problems have numbers and words in the solution. For example, when measuring, be sure to use accurate units of measurement. 7) Look for and make use of structure.

Use what you know about numbers and patterns to solve unknown problems. Look closely at the problem to recognize patterns or configurations that make sense and can be used to find a solution. 8) Look for and express regularity in repeated reasoning. Notice number patterns and check for logical answers. Real-world problem solvers look for repeated situations or calculations in order to find shortcuts or general strategies to solving the problem. Find the value.1) 103 = __________________________________________________________________________________ 2) 3 104 = ______________________________________________________________________________ 3) 24 102 = _____________________________________________________________________________ 4) 8 100 = ______________________________________________________________________________ 5) 7 103 = ______________________________________________________________________________ 6) 10 10 10 10 = _____________________________________________________________________ 7) 10 10 10 = _________________________________________________________________________ 8) 43 105 = _____________________________________________________________________________ 9) 102 = __________________________________________________________________________________ 10) 17 104 = ____________________________________________________________________________ Use place value patterns to complete the table.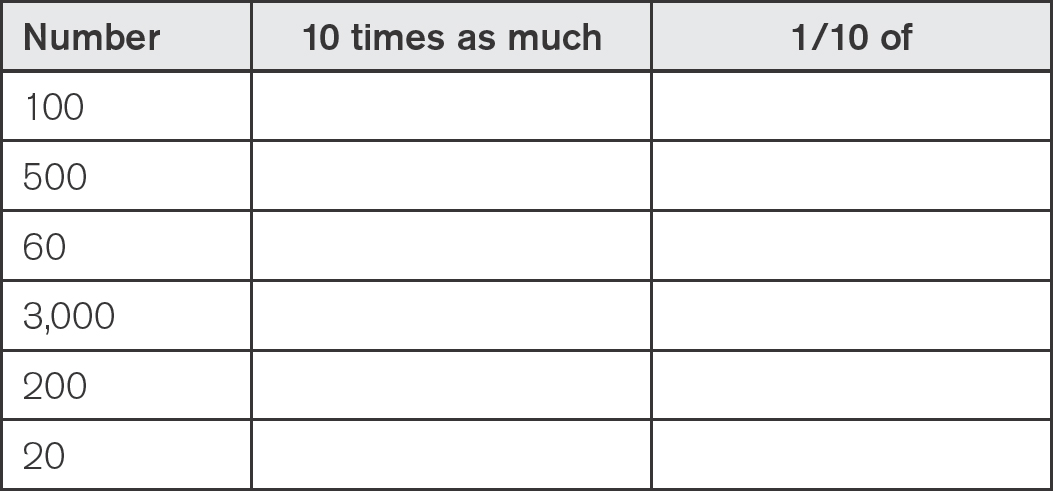Write the value of the underlined digit.1) 45,278 ________________________________________________________________________________ 2) 3,690 _________________________________________________________________________________ 3) 35 ___________________________________________________________________________________ 4) 1,73,739 ______________________________________________________________________________