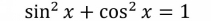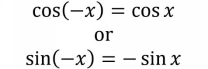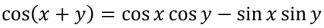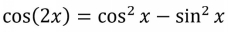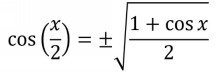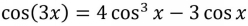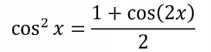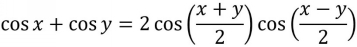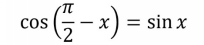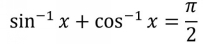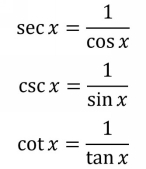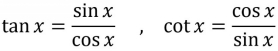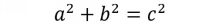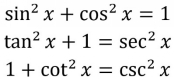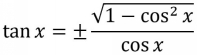Chris McMullen - Trig Identities Practice Workbook with Answers: 10 (Improve Your Math Fluency)

Trig Identities Practice Workbook with Answers: 10 (Improve Your Math Fluency) — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Trig Identities Practice Workbook with Answers: 10 (Improve Your Math Fluency)" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...10

TRIG IDENTITIES

Practice Workbook

with Answers

Chris McMullen, Ph.D.

Copyright 2020 Chris McMullen, Ph.D.

monkeyphysicsblog.wordpress.com

improveyourmathfluency.com

chrismcmullen.com

All rights reserved.

Zishka Publishing

ISBN: 978-1-941691-38-0

Mathematics > Trigonometry

Mathematics > Precalculus

CONTENTS

Introduction

This workbook helps students understand a variety of standard trig identities. Each chapter begins with a concise introduction to pertinent concepts and includes fully solved examples to help serve as a guide. Hints and answers to the problems can be found at the back of the book. The following kinds of trig identities are covered:

A Pythagorean identity follows from the Pythagorean theorem. For example,

can be derived by applying the Pythagorean theorem to a right triangle.

An odd/even function identity refers to identities such as

Each of the six standard trig functions (sine, cosine, tangent, secant, cosecant, and cotangent) is either an even function or an odd function.

An angle sum identity involves the sum (or difference) of two angles in the argument of a trig function, like

In a double angle identity, the argument of one trig function has twice the angle of another trig function, such as

In a half-angle identity, the argument of one trig function has one-half the angle of another trig function, such as

In a multiple angle identity, the argument of one trig function is a multiple of the angle of another trig function, like

In a power reduction identity, a power of a trig function is expressed in terms of smaller powers of trig functions, like

Sum/product identities relate the sum of two trig functions to the product of two trig functions, like

Angle shifting identities shift the angle, like

The law of sines and law of cosines apply even to acute or obtuse triangles.

An inverse function identity involves an inverse trig function, such as

1 Pythagorean Identities

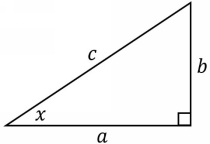
Recall that the standard trig functions relate the sides of a right triangle. The longest side is the hypotenuse ; it is opposite to the right angle. One leg is called the opposite side; it is opposite to the angle in the argument of the trig function. The other leg is called the adjacent side; the angle in the argument of the trig function is formed by the adjacent and the hypotenuse. The six standard trig functions are the cosine, sine, tangent, secant, cosecant, and cotangent.

Note that secant and cosine are reciprocals, sine and cosecant are reciprocals, and tangent and cotangent are reciprocals. (Although some students intuitively expect the cosecant and cosine to go together because they both have cos in their names, these two functions are not reciprocals. The cosecant function is the reciprocal of the sine function, whereas the secant function is the reciprocal of the cosine function.)

Also note that tangent and cotangent can be expressed as the following quotients:

According to the Pythagorean theorem , which applies to every right triangle, the square of the adjacent side plus the square of the opposite side equals the square of the hypotenuse. For example, for the right triangle shown below, the hypotenuse is c, the side opposite to x is b, and the side adjacent to x is a. The Pythagorean theorem for this right triangle is:

The definitions of the standard trig functions can be combined with the Pythagorean theorem to form the following Pythagorean identities . We will derive the first identity in Example 1; the others will be explored in the exercises.

The above identities (along with the reciprocal identities for secant, cosecant, and cotangent from the previous page) allow any trig function to be expressed exclusively in terms of any other trig function. For example, we can express the tangent function in terms of the cosine function as

(see Example 2). We will explore other trig identities of this nature in the exercises.

Example 1 . Derive

Solution . Consider the right triangle shown above. The Pythagorean theorem is:

Next page

1234567...10

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Trig Identities Practice Workbook with Answers: 10 (Improve Your Math Fluency)»

Look at similar books to Trig Identities Practice Workbook with Answers: 10 (Improve Your Math Fluency). We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Kaplan Test Prep

SAT Math Prep: Over 400 Practice Questions + Online

Chris McMullen

Essential Prealgebra Skills Practice Workbook

Chris McMullen

Geometry Proofs Essential Practice Problems Workbook with Full Solutions (Improve Your Math Fluency)

Chris McMullen

Fractions Essentials Workbook with Answers (Improve Your Math Fluency)

Chris McMullen

Essential Modern Physics Study Guide Workbook

Jerry Ortner

Frustrations with Math

Kaplan Test Prep

SAT Math Prep

McMullen

Calculus: Essential calculus skills practice workbook with full solutions

Yang Kuang

Pre-Calculus Workbook For Dummies

Forseth Krystle Rose

Pre-Calculus For Dummies

Chris McMullen

50 Challenging Calculus Problems (Fully Solved)

Mary Jane Sterling

Trigonometry for Dummies

Discussion, reviews of the book Trig Identities Practice Workbook with Answers: 10 (Improve Your Math Fluency) and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.