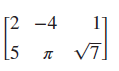Page A-1
Additional Topics Appendix
Section A.1 Additional Factoring Concepts Factoring by Using
Substitution Factoring 1 Term with 3 Terms Additional Factoring
Strategies 1. Factoring by Using Substitution The trinomial u 2 + u has a leading coefficient 1 and factors as ( u + )( u ). Now compare the following polynomials to u 2 + u In each case, the variable expressions in the first and second terms are the same. Furthermore, the coefficients are 1, 4, and By letting the single variable u represent the variable expression in parentheses, the polynomial is a quadratic trinomial in u.

With an appropriate substitution, the polynomials are easier to factor. ( a + b )2 + ( a + b ) Solution:

Skill Practice Factor completely. ( w )2( w ) In Examples 2 and 3, we use substitution to factor a difference of squares and a sum of cubes. ( w )2( w ) In Examples 2 and 3, we use substitution to factor a difference of squares and a sum of cubes.
Example 2 Factoring by Using Substitution Factor completely. ( x )2 Solution:  Skill Practice Factor completely. ( x + ) Example 3 Factoring by Using Substitution Factor completely. ( x + )3 + Solution:
Skill Practice Factor completely. ( x + ) Example 3 Factoring by Using Substitution Factor completely. ( x + )3 + Solution: 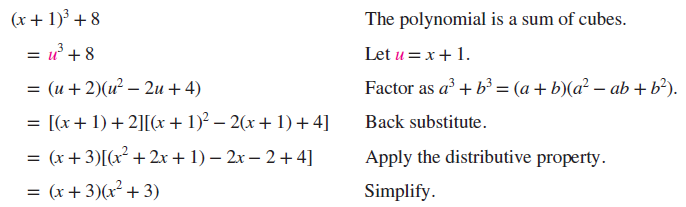 Skill Practice Factor completely. ( y + )3 + Answers ( x )( x + ) ( y + )( y + y + ) 2. Factoring 1 Term with 3 Terms When confronted with a 4-term polynomial, sometimes the standard method of grouping does not apply.
Skill Practice Factor completely. ( y + )3 + Answers ( x )( x + ) ( y + )( y + y + ) 2. Factoring 1 Term with 3 Terms When confronted with a 4-term polynomial, sometimes the standard method of grouping does not apply.
For example, consider the polynomial x 2 y 2 y Notice that grouping 2 terms with 2 terms does not result in common binomial factors. 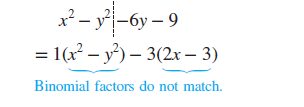 However, if a factor of is removed from the last three terms, the last three terms result in a perfect square trinomial. This is called grouping 1 term with 3 terms. Page A-3 Example 4 Factoring by Grouping 1 Term with 3 Terms Factor completely. x 2 y 2 y Solution: This polynomial has 4 terms.
However, if a factor of is removed from the last three terms, the last three terms result in a perfect square trinomial. This is called grouping 1 term with 3 terms. Page A-3 Example 4 Factoring by Grouping 1 Term with 3 Terms Factor completely. x 2 y 2 y Solution: This polynomial has 4 terms.  Skill Practice Factor completely. n 2 m 2 m Answer ( n + m + )( n m ) The difference of squares ( x )2( y + )2 can also be factored without using a substitution. ( x )2( y + )2
Skill Practice Factor completely. n 2 m 2 m Answer ( n + m + )( n m ) The difference of squares ( x )2( y + )2 can also be factored without using a substitution. ( x )2( y + )2
= [ x + ( y + )] [ x ( y + )]
= ( x + y + )( x y ) 3. ( x )2( y + )2
= [ x + ( y + )] [ x ( y + )]
= ( x + y + )( x y ) 3.
Additional Factoring Strategies Thus far, we have learned how to factor polynomials that fit the following patterns. Difference of squares Difference of cubes Sum of cubes Perfect square trinomials Nonperfect square trinomials Grouping 2 terms by 2 terms Grouping 3 terms by 1 term Many polynomials do not fit any of these patterns, and many polynomials do not factor using these techniques. However, sometimes a combination of patterns exists and we can find the factored form. In Example 5, the polynomial has 6 terms. We might try grouping 3 terms with 3 terms or 4 terms with 2 terms, or even 2 terms, 2 terms and 2 terms. In any case, we should expect to try a variety of approaches before a workable strategy is identified.
Page A-4 Example 5 Factoring a Polynomial Factor completely. a c + a b c b c Solution:  Skill Practice Factor completely. x y + y + x z + z x Answer ( x + )( y + z ) Section A.1 Practice Exercises Vocabulary and Key Concepts x Given the expression ( x )2( x ) , what substitution could be used for u to make this a simpler quadratic trinomial in terms of u ? Given the expression ( p )2 , what substitution could be used for u to make this a simpler difference of squares in terms of u ? What would be the first step to factor x 2 x + y 2 by grouping 3 terms with 1 term?
Skill Practice Factor completely. x y + y + x z + z x Answer ( x + )( y + z ) Section A.1 Practice Exercises Vocabulary and Key Concepts x Given the expression ( x )2( x ) , what substitution could be used for u to make this a simpler quadratic trinomial in terms of u ? Given the expression ( p )2 , what substitution could be used for u to make this a simpler difference of squares in terms of u ? What would be the first step to factor x 2 x + y 2 by grouping 3 terms with 1 term?
What would be the first two steps to factor a 2 b 2 b by grouping 1 term with 3 terms?
Concept 1: Factoring by Using Substitution For Exercises 520, factor completely. (See Examples 13.) (4t1)2 + 3(4t1)- 4 (2p + 5)24(2p + 5)- 12 2(w2)25(w2)- 3 3(y + 4)2 + 11(y + 4)- 4 25(x + 4)2y2 36(y5)2z2 9(5a3)24 25(3b + 7)216 (t2)2(2t + 1)2 (w + 3)2(3w5)2 (a + b)3 + c3 (x + 4)3y3 27c3(d + 2)3 125v3 + (w1)3 4x2 + 28x(2y + 1) + 49(2y + 1)2 9a212a(b + 1) + 4(b + 1)2 Page A-5 Concept 2: Factoring 1 Term with 3 Terms For Exercises 2128, factor completely. (See Example 4.) x210x + 25y2 m222m + 121n2 a2x218xy81y2 c2a2 + 16ab64b2 25a2 + 20ab + 4b2100c2 36x2 + 60xy + 25y2121z2 64w29t 2 + 24tp16p2 49k225m2 + 30mn9n2 Concept 3: Additional Strategies and Mixed Exercises For Exercises 2968, factor completely. (See Examples 1 ) x24y2x2y 9v2w23v + w w7 + 8w4w38 t 5125t 24t 3 + 500 xy4x + 2yz8z2y + 8 ax + 4a + 2bx + 8bcx4c x2 + xy2y2 + xy a2 + 2ab3b2b + a n663n364 m6 + 7m38 (a + b)26(a + b )( cd) + 9(cd)2 (x + 1)24(x + 1 )( x2) + 4(x2)2 4x410x336x2 + 90x 15x45x360x2 + 20x a2 + 2ab + b2ab v2 + 6vw + 9w2v3w x2(x + y)- y2(x + y) u2(uv)- v2(uv) (a + 3)4 + 6(a + 3)3 (4b)42(4b)3 24(3x + 5)330(3x + 5)2 10(2y + 3)2 + 15(2y + 3) 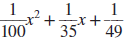
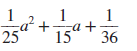 (5x21)24(5x21)- 5 (x3 + 4)210(x3 + 4) + 24 16p4q4 s4t 481
(5x21)24(5x21)- 5 (x3 + 4)210(x3 + 4) + 24 16p4q4 s4t 481 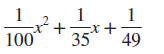
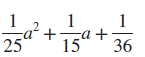 6a3 + a2b6ab2b3 4p3 + 12p2qpq23q3
6a3 + a2b6ab2b3 4p3 + 12p2qpq23q3 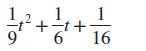
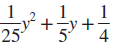 6ax + 2bxby3ay 5pq4q12 + 15p x81 y8256 25c29d 2 + 5c3d 5wx3 + 5wy32zx32zy3 Page A-6 Section A.2 Solving Systems of Linear Equations by Using Matrices Concepts 1.Introduction to Matrices 2.Solving Systems of Linear Equations by Using the Gauss-Jordan Method 1.
6ax + 2bxby3ay 5pq4q12 + 15p x81 y8256 25c29d 2 + 5c3d 5wx3 + 5wy32zx32zy3 Page A-6 Section A.2 Solving Systems of Linear Equations by Using Matrices Concepts 1.Introduction to Matrices 2.Solving Systems of Linear Equations by Using the Gauss-Jordan Method 1.
Introduction to Matrices We have already learned how to solve systems of linear equations by using the substitution method and the addition method. We now present a third method called the Gauss-Jordan method that uses matrices to solve a linear system. A matrix is a rectangular array of numbers (the plural of matrix is matrices ). The rows of a matrix are read horizontally, and the columns of a matrix are read vertically. Every number or entry within a matrix is called an element of the matrix. The order of a matrix is determined by the number of rows and number of columns.
A matrix with m rows and n columns is an mn (read as m by n ) matrix. Notice that with the order of a matrix, the number of rows is given first, followed by the number of columns. Example 1 Determining the Order of a Matrix Determine the order of each matrix. a. 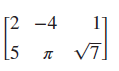
Next page












 With an appropriate substitution, the polynomials are easier to factor. ( a + b )2 + ( a + b ) Solution:
With an appropriate substitution, the polynomials are easier to factor. ( a + b )2 + ( a + b ) Solution:  Skill Practice Factor completely. ( w )2( w ) In Examples 2 and 3, we use substitution to factor a difference of squares and a sum of cubes. ( w )2( w ) In Examples 2 and 3, we use substitution to factor a difference of squares and a sum of cubes.
Skill Practice Factor completely. ( w )2( w ) In Examples 2 and 3, we use substitution to factor a difference of squares and a sum of cubes. ( w )2( w ) In Examples 2 and 3, we use substitution to factor a difference of squares and a sum of cubes.  Skill Practice Factor completely. ( x + ) Example 3 Factoring by Using Substitution Factor completely. ( x + )3 + Solution:
Skill Practice Factor completely. ( x + ) Example 3 Factoring by Using Substitution Factor completely. ( x + )3 + Solution: 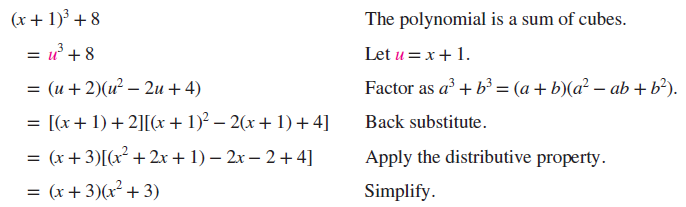 Skill Practice Factor completely. ( y + )3 + Answers ( x )( x + ) ( y + )( y + y + ) 2. Factoring 1 Term with 3 Terms When confronted with a 4-term polynomial, sometimes the standard method of grouping does not apply.
Skill Practice Factor completely. ( y + )3 + Answers ( x )( x + ) ( y + )( y + y + ) 2. Factoring 1 Term with 3 Terms When confronted with a 4-term polynomial, sometimes the standard method of grouping does not apply.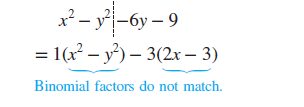 However, if a factor of is removed from the last three terms, the last three terms result in a perfect square trinomial. This is called grouping 1 term with 3 terms. Page A-3 Example 4 Factoring by Grouping 1 Term with 3 Terms Factor completely. x 2 y 2 y Solution: This polynomial has 4 terms.
However, if a factor of is removed from the last three terms, the last three terms result in a perfect square trinomial. This is called grouping 1 term with 3 terms. Page A-3 Example 4 Factoring by Grouping 1 Term with 3 Terms Factor completely. x 2 y 2 y Solution: This polynomial has 4 terms.  Skill Practice Factor completely. n 2 m 2 m Answer ( n + m + )( n m ) The difference of squares ( x )2( y + )2 can also be factored without using a substitution. ( x )2( y + )2
Skill Practice Factor completely. n 2 m 2 m Answer ( n + m + )( n m ) The difference of squares ( x )2( y + )2 can also be factored without using a substitution. ( x )2( y + )2 Skill Practice Factor completely. x y + y + x z + z x Answer ( x + )( y + z ) Section A.1 Practice Exercises Vocabulary and Key Concepts x Given the expression ( x )2( x ) , what substitution could be used for u to make this a simpler quadratic trinomial in terms of u ? Given the expression ( p )2 , what substitution could be used for u to make this a simpler difference of squares in terms of u ? What would be the first step to factor x 2 x + y 2 by grouping 3 terms with 1 term?
Skill Practice Factor completely. x y + y + x z + z x Answer ( x + )( y + z ) Section A.1 Practice Exercises Vocabulary and Key Concepts x Given the expression ( x )2( x ) , what substitution could be used for u to make this a simpler quadratic trinomial in terms of u ? Given the expression ( p )2 , what substitution could be used for u to make this a simpler difference of squares in terms of u ? What would be the first step to factor x 2 x + y 2 by grouping 3 terms with 1 term?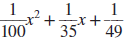
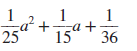 (5x21)24(5x21)- 5 (x3 + 4)210(x3 + 4) + 24 16p4q4 s4t 481
(5x21)24(5x21)- 5 (x3 + 4)210(x3 + 4) + 24 16p4q4 s4t 481 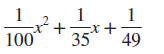
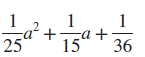 6a3 + a2b6ab2b3 4p3 + 12p2qpq23q3
6a3 + a2b6ab2b3 4p3 + 12p2qpq23q3 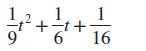
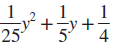 6ax + 2bxby3ay 5pq4q12 + 15p x81 y8256 25c29d 2 + 5c3d 5wx3 + 5wy32zx32zy3 Page A-6 Section A.2 Solving Systems of Linear Equations by Using Matrices Concepts 1.Introduction to Matrices 2.Solving Systems of Linear Equations by Using the Gauss-Jordan Method 1.
6ax + 2bxby3ay 5pq4q12 + 15p x81 y8256 25c29d 2 + 5c3d 5wx3 + 5wy32zx32zy3 Page A-6 Section A.2 Solving Systems of Linear Equations by Using Matrices Concepts 1.Introduction to Matrices 2.Solving Systems of Linear Equations by Using the Gauss-Jordan Method 1.