GRAPH
THEORY
Ronald Gould
Goodrich C. White Professor
Department of Mathematics and Computer Science
Emory University
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 2012 by Ronald Gould
All rights reserved.
Bibliographical Note
This Dover edition, first published in 2012, is a corrected republication of the work first published in 1988 by the Benjamin-Cummings Publishing Company, Menlo Park, California.
Library of Congress Cataloging-in-Publication Data
Gould, Ronald, author.
Graph theory / Ronald Gould. Dover edition.
pages cm. (Dover books on mathematics)
Summary: An introductory text in graph theory, this treatment covers primary techniques and includes both algorithmic and theoretical problems. Algorithms are presented with a minimum of advanced data structures and programming details. This thoroughly corrected 1988 edition provides insights to computer scientists as well as mathematicians studying topology, algebra, and matrix theory Provided by publisher.
Includes bibliographical references and index.
eISBN-13: 978-0-486-32036-6
1. Graph theory. I. Title.
QA166.G66 2012
511.5dc23
2012022298
Manufactured in the United States by Courier Corporation
49806901
www.doverpublications.com
To Lyn and Dad,
For their love, support and patience.
Preface
This text is intended to be an introductory text in graph theory. As such, I feel it must reflect as many of the diverse aspects of this growing subject as possible. However, it was impossible to include every topic. Thus, I tried to concentrate on well-established topics, reflecting the primary techniques used in the study of graphs. Being both a mathematician and a computer scientist certainly colored my thinking. Fundamental to my thinking is a belief that both a firm algorithmic background as well as a theoretical background are needed. I have tried to include as many fundamental algorithms as possible, while still maintaining a foundation in standard theoretical results. I have also included as many proofs about both the algorithmic and theoretical results as seemed reasonable. The exercises include both theoretic and algorithmic problems. However, so that this text would be accessible to as many students as possible, the algorithms are presented with a minimum of advanced data structures or programming details.
The table below shows the sections I feel will form the core of a typical undergraduate junior or senior level course. The remaining sections are included to supplement these topics, allowing the instructor to tailor the class to his or her own tastes, and to allow this text to also be used in a year-long sequence or by a beginning graduate class. The only prerequisites are a fundamental understanding of elementary proof techniques, such as induction or proof by contradiction. An absolute minimum amount of algebra is necessary, as well as a minimal understanding of algorithms. Little beyond matrix multiplication is ever used. No prior programming skills are required, but, of course, such skills can only help.
Typical Undergraduate Class |
Chapter | Sections |
| 1.1 1.2 1.3 1.4 1.5 1.6 |
| 2.1 2.2 2.3 2.4 |
| 3.1 3.2 3.3 3.5 |
| 4.1 4.2 4.5 4.6 |
| 5.1 5.2 5.3 5.5 5.6 |
| 6.1 6.2 6.3 |
| 7.1 7.2 7.3 |
| 8.1 8.2 8.3 8.4 8.5 8.6 |
Substitutions are certainly possible to give the class a more theoretic or a more algorithmic flavor. Topics from , is intended for graduate students.
. Thus, I hope you will find a surprise or two along the way.
I would like to thank Craig Bartholomew, Sally Elliott and Sharon Montooth for their editorial assistance. I would also like to thank Peter Winkler, Tom Trotter, Dwight Duffus, Mike Jacobson, Ralph Faudree, Roger Entringer, Buck McMorris and Ken Mandelberg for their helpful comments, suggestions and assistence. I would like to blame all errors on my typist, Ronald Gould, and my typesetter, R. Gould. I am sure the text was perfect until they got their hands on it.
Ron Gould
Chapter 1
Graphs
Section 1.0 Introduction
For years, mathematicians have affected the growth and development of computer science. In the beginning they helped design computers for the express purpose of simplifying large mathematical computations. However, as the role of computers in our society changed, the needs of computer scientists began affecting the kind of mathematics being done.
Graph theory is a prime example of this change in thinking. Mathematicians study graphs because of their natural mathematical beauty, with relations to topology, algebra and matrix theory spurring their interest. Computer scientists also study graphs because of their many applications to computing, such as in data representation and network design. These applications have generated considerable interest in algorithms dealing with graphs and graph properties by both mathematicians and computer scientists.
Today, a study of graphs is not complete without at least an introduction to both theory and algorithms. This text will attempt to convince you that this is simply the nature of the subject and, in fact, the way it was meant to be treated.
Section 1.1 Fundamental Concepts and Notation
Graphs arise in many settings and are used to model a wide variety of situations. Perhaps the easiest way to adjust to this variety is to see several very different uses immediately. Initially, lets consider several problems and concentrate on finding models representing these problems, rather than worrying about their solutions.
Suppose that we are given a collection of intervals on the real line, say C = { I1, I2,... , Ik}. Any two of these intervals may or may not have a nonempty intersection. Suppose that we want a way to display the intersection relationship among these intervals. What form of model will easily display these intersections?
One possible model for representing these intersections is the following: Let each interval be represented by a circle and draw a line between two circles if, and only if, the intervals that correspond to these circles intersect. For example, consider the set
C = { [4, 2], [0, 1], (8, 2], [2, 4], [4, 10) }.
The model for these intervals is shown in .
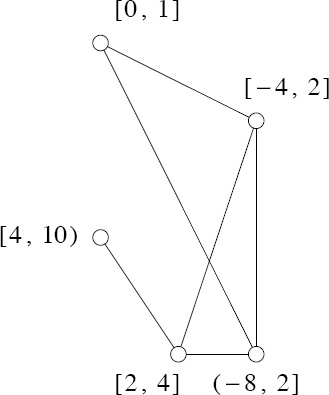
Figure 1.1.1. A model for the intersections of the members of C.
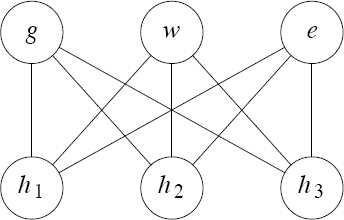
Next, we consider the following old puzzle. Suppose there are three houses (call them h1, h2 and h3) and three utility companies (say gas (g), water (w) and electricity (e)). Our problem is to determine if it is possible to connect each of the three houses to each of the three utilities without crossing the service lines that run from the utilities to the houses. We model this puzzle by representing each house and each utility as a circle and drawing a line between two circles if there is a service line between the corresponding house and utility. We picture this situation in is not a solution to the problem, but merely an attempt at modeling the problem.