Nora Hartsfield - Pearls in Graph Theory: A Comprehensive Introduction

PEARLS IN
GRAPH THEORY

A Comprehensive Introduction

A Comprehensive Introduction

Nora Hartsfield

Department of Mathematics

Western Washington University

Bellingham, Washington

Gerhard Ringel

Department of Mathematics

University of California

Santa Cruz, California

DOVER PUBLICATIONS, INC.

Mineola, New York

Copyright

Copyright 1990, 1994 by Nora Hartsfield and Gerhard Ringel

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2003, is an unabridged republication (with one figure newly corrected by the authors) of the revised and augmented edition published by Academic Press, San Diego and London, in 1994. The work was originally published by Academic Press in 1990.

International Standard Book Number: 0-486-43232-7

Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501

When we wrote the original Pearls in Graph Theory, we had in mind several goals. Among these were clarity and simplicity, to make the book accessible to students with minimal prerequisites; a length and selection of topics compatible with a single term course; and a variety of exercises ranging in difficulty from elementary to challenging.

In revising the book, we wanted to preserve the original spirit with respect to length and clarity. The changes that we made include correcting errors, improving certain of the proofs, changing and adding illustrations, and adding many more exercises. Thus we feel that we have polished Pearls without disturbing the goals we achieved in the initial work and without disturbing the essential character of the book.

What is a pearl? It could be a graph, theorem, proof, conjecture, or exercise that provokes thought, causes surprise, stimulates interest, or inspires further research. We have collected as many pearls as possible in this book with the hope of maximizing the pleasure for both the teacher and the student. Consequently, students will find themselves receptive to new and challenging mathematical concepts. Historically, many areas of graph theory have developed from recreational mathematics. This entertainment factor can be used as a stimulant to the student and provide him or her with a new view of mathematics.

Combinatorics and graph theory are fast growing fields. Increasing numbers of courses are being taught at the undergraduate and graduate levels, and the wide variety of applications has increased the popularity of graph theory in other fields, including the natural sciences, engineering, genetics, and even in such social sciences as psychology and sociology. Mathematicians also find that employing graphs in their work facilitates the understanding and solving of problems encountered in their research.

Gerhard Ringel has taught courses in combinatorics at the University of California at Santa Cruz since 1970. At first his students consisted only of mathematics majors but, as the years passed, more and more computer science students joined his courses. The study of graph theory is now becoming essential for computer science majors. It is of fundamental importance to the understanding of abstract data structures and of the complexity and analysis of algorithms.

Prerequisites for this book are a strong interest in the subject and a good foundation in high school mathematics. A course in discrete mathematics is recommended but not necessary.

The exercises following each section have been designed to implement the concepts of the section and, we hope, to motivate further study. The starred exercises are considered particularly challenging.

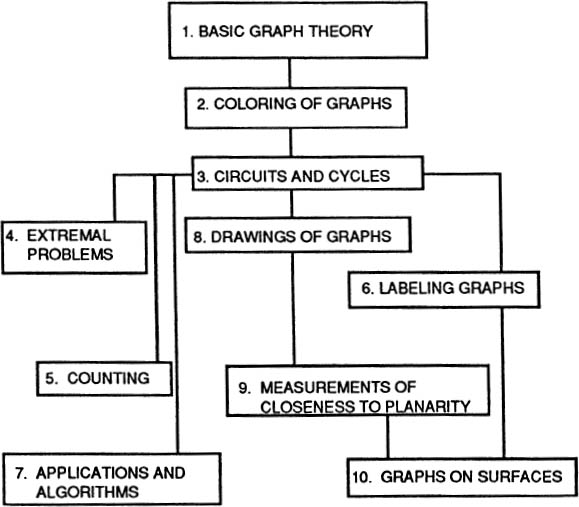
The following chart explains the relationship among the chapters of the book. is the most interesting and should not be omitted from any course.

Before we give any definitions and theory, let us consider the following example. There is a basket containing an apple, a banana, a cherry and a date. Four children named Erica, Frank, Greg and Hank are each to be given a piece of the fruit. Erica likes cherries and dates; Frank likes apples and cherries; Greg likes bananas and cherries; and Hank likes apples, bananas, and dates. as an aid to solving the problem.

is greatly simplified, of course. It shows some different ways of driving from San Jose to San Francisco.

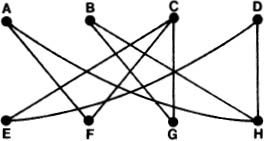
Figure 1.1.1

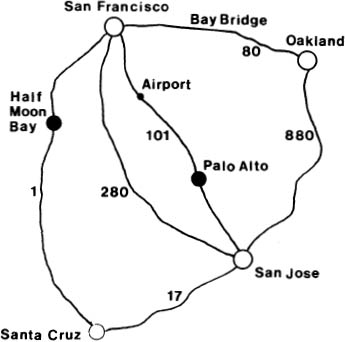
Figure 1.1.2

Chemists use diagrams to picture molecules, and these diagrams are also graphs. Usually the hydrogen atoms are omitted from the diagrams by the chemists using shorthand structure, but the Kekul structure includes them.

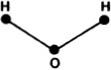
Figure 1.1.3. Water, H2O.

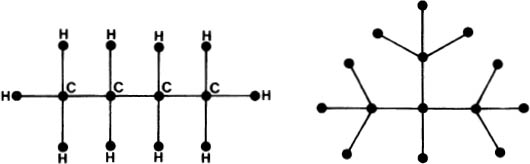
Figure 1.1.4. Butane and isobutane, C4H10.

In for another molecule C60.

Graph theory is used in designing printed circuits for use in electronics devices. Circuits printed on silicon chips must be designed differently from those using insulated wires, since the conducting portions cannot cross one another. The graph of shows part of a printed circuit used in a computer.

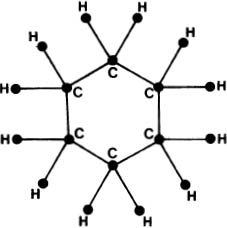
Figure 1.1.5. Cyclohexane, C6H12.

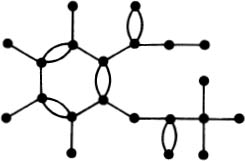
Figure 1.1.6. Aspirin, C9H8O4.

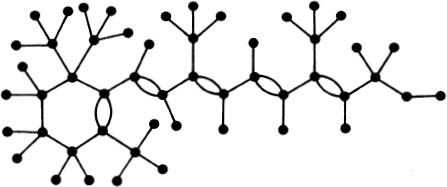
Figure 1.1.7. Vitamin A, C20H30O.

Algorithms can also be described by graphs. The graph of is a chart of the steps used in an algorithm for solving a certain problem using a computer.

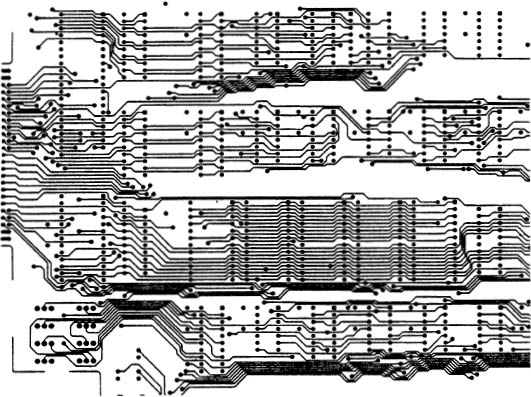
Figure 1.1.8. Portion of a printed circuit

Figure 1.1.9

In the study of lattices and Boolean algebras, graphs arise as diagrams of these structures. Those who have studied set theory will recognize the diagrams of show all subsets of the set at the top. If one set is derived from another by deleting one element, then the two sets are connected by a line in the diagram.