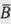Every area of mathematics makes use to some extent of the concepts set, relation, and function. Graph theory not only involves these concepts, but, in fact, set and relation are fundamental to the meaning of the word graph itself. It is therefore essential that we clearly understand these terms. As with every other mathematical subject, the theory of graphs develops through theorems and proofs. We also include a brief discussion of this important topic.
A.1 Sets and Subsets
We give no technical definition of the concept of set, for any attempt to define set only uses words whose meaning is synonymous with set itself, such as collection or family. We say that a set is composed of elements, but we will not attempt to define this term either. We will soon clarify how these words are employed.
To describe a set, we list its elements, if this is feasible, or we may present some rule indicating precisely those elements belonging to the set. For example, we may refer to the set of students taking this class. If the number of students is not very large, we can describe this same set by listing the individuals; however, a listing of the students does not suggest what these people have in common, namely that they are all members of this class. Hence we may prefer to describe a set by means of a rule (if possible), independent of the number of elements in the set.
For the most part, we shall use capital (upper case) letters to denote a set, such as U or V, and lower case letters to represent the elements of a set. The notation u U indicates that u is an element of U, while v , v V implies that v and v are both elements of the set V. If w is not an element of W, we write w W. To indicate that a set U consists of the elements u1, u2 and u3, we write U = { u , u 2, u }. If N denotes the natural numbers (positive integers), then
V = { v i1 i 100, i N }
means that V consists of the 100 elements v , v , etc., up to and including v 100. More formally, this is read as the set of all elements vi such that [the vertical bar means such that] 1 i 100 and i N . Indeed, this same set V could be described equally well by writing
V = { v 1, v 2,... , v 100},
V = { v i i = 1, 2,... , 100},
or
V = { v i1 i 100},
since it is understood that i N .
If U and V are sets with the property that every element of U is an element of V , then we say U is a subsets of V, and write U V . If U and V contain precisely the same elements, then U and V are equal sets, denoted U = V. The statement U = V is equivalent to saying U V and V U .
In accord with the preceding statements,
{ u , u , u } = { u , U } = { u , u };
that is, the composition of a set is not affected by an element listed more than once, nor by the order in which elements are listed. If U V and U V (that is, U is not equal to V ), then every element of U is an element of V , but at least one element of V does not belong to U. Under these conditions, we say U is a proper subset of V, and write U V. A set may have no elements; if this is the case, we designate the set by and call it the null set or empty set. For every set W, it follows that W; for if this were not the case, there would exist an element x such that x and x W. However, this is impossible since contains no elements.
In any particular discussion concerning sets, the sets involved are usually subsets of some specified set, called the universal set. For example, at a certain time we may be interested in sets of positive integers; in this case, the universal set is N. If U denotes the universal set on some occasion and S is a subset of U, then the complement 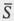 of S is that set consisting of all elements of U not belonging to S , i.e.,
of S is that set consisting of all elements of U not belonging to S , i.e.,
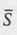 = { x U x S }.
= { x U x S }.
Note that U = .
Given two sets V and W, the union of V and W, denoted V W , is the set consisting of elements belonging to V or W (or both). The intersection V W of V and W is the set containing those elements belonging to both V and W. If V n W = , then we say V and W are disjoint sets (meaning that V and W have no elements in common). As an illustration, let
U = { u , u , u }, V = { u , u }, and W = { u , u }.
Then
U V = { u , u , u }, U V = { u , u },
V W = { u , u , u , u }, U W = { u }, and V W = .
Therefore, V and W are disjoint.
Two famous set equalities involving complements, unions, and intersections are called DeMorgans Laws, stated next. We prove the first of these laws and leave the proof of the second as an exercise.
Theorem A.1
(DeMorgans Laws)
Let U be the universal set, and let A and B be subsets of U. Then:
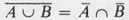
 .
.
Proof of (a)
We give the proof in two parts; specifically, we show 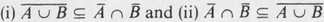 .
.
To prove (i), we let x 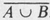 . Then x U but x A B. Since x A B, the element x belongs to neither A nor B, i.e., x A and x B. This implies that x
. Then x U but x A B. Since x A B, the element x belongs to neither A nor B, i.e., x A and x B. This implies that x 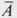 and x
and x 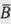

















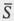 of S is that set consisting of all elements of U not belonging to S , i.e.,
of S is that set consisting of all elements of U not belonging to S , i.e.,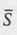 = { x U x S }.
= { x U x S }.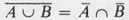
 .
.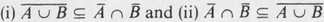 .
.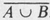 . Then x U but x A B. Since x A B, the element x belongs to neither A nor B, i.e., x A and x B. This implies that x
. Then x U but x A B. Since x A B, the element x belongs to neither A nor B, i.e., x A and x B. This implies that x 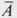 and x
and x