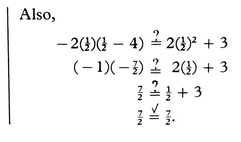Bonnie Averbach - Problem solving through recreational mathematics

Like most authors, we are indebted to many people who have assisted us in a variety of ways from the time our idea for this book was first conceived until final publication.

For their advice, encouragement, and many helpful suggestions, we would like to thank David Blauer, Isidor Chein, Martin Gardner, Nancy Hagelgans, William Karjane, Archibald Krenzel, Robert Morse, Leon Steinberg, William Traylor, William Wisdom, and David Zitarelli, as well as the reviewers who read our manuscript at various stages during its preparation and the editors who worked with us during the production process.

We would also like to thank Raelaine Ballou for her continual assistance in tracking down some of the many sources we used in preparing our manuscript, Susan Graham for drawing preliminary sketches for many of our cartoon ideas, John Johnson for embellishing these ideas and bringing them to their delightful final form, and Nadia Kravchenko for her excellent typing of the entire manuscript.

For their constant encouragement and patience throughout the years we were writing this book, we extend our love and thanks to the members of our familiesRachelle, Wayne, Debra, Gary, Robert, Stephen, Jake, and Alex Averbach, and Carrie,Adam, and Jason Chein.

The origins of many mathematical problems are lost in the mists of antiquity; thus our attempts to locate original sources for our problems were not very successful. We decided to settle for identifying those sources from which we have taken problems essentially verbatim. Each such problem in the text is followed by a reference number, which refers to a source appearing in the Bibliography. In particular, we would like to acknowledge the following publishers and authors for granting us permission to reprint or adapt some of their material.

Exercises 1.19 and 1.22 are reprinted with the permission of Al B. Perlman. Problem 4.4 and Exercises 5.9 and 7.22 have been adapted from Mathematical Puzzles for Beginners and Enthusiasts by Geoffrey Mott-Smith (copyright 1946 by Copeland and Lamm, Inc., copyright renewed in 1974; published by Dover Publications, Inc.), with the permission of Copeland and Lamm, Inc. Problem 8.2 and its solution and Exercise 8.9 have been adapted from Polyominoes by Solomon W. Golomb (copyright 1965 by Solomon W. Golomb), with the permission of Charles Scribners Sons and Allen & Unwin, Ltd.

Dover Publications has granted us permission to use problems from several of the books in their fine series on mathematical recreations. In particular, we have taken problems from the Dover books by Friedland, Kraitchik, Phillips, and Read listed in our Bibliography, and also from Mathematical Bafflers by Angela Dunn, some of whose material was published earlier by Litton Industries in their Problematical Recreations series.

Several journals have also been helpful: Technology Review, with its Puzzle Corner edited by Allan Gottlieb; Arithmetic Teacher; Mathematics Magazine ; and Sphinx: Revue Mensuelle des Questions Recreatives, edited by M. Kraitchik and M. Pigeolet.

The American Mathematical Society, Emerson Books, Inc., the Longman Group Limited, and McGraw-Hill, Inc. also granted permission for use of problems.

Finally, we wish to thank Phillip Matthew Swift for his work in graphics and word processing to prepare the new chapter on probability (Appendix C) for this edition.

B.A.
O.C.

Appendix A

Some Basic Algebraic Techniques

The a B ility to solve algebraic equations is one of the most important of mathematical skills. In this appendix, we review some of the standard basic techniques:

1. How to solve a linear equation in one unknown.
2. How to solve a linear inequality in one unknown.
3. How to use the quadratic formula to solve a quadratic equation in one unknown.
4. How to use factoring to solve a quadratic equation in one unknown.
5. How to use the substitution method to solve a simultaneous system of two linear equations in two unknowns.
6. How to use the method of elimination to solve a simultaneous system of two linear equations in two unknowns.
7. How to solve a simultaneous system of three linear equations in three unknowns.
8. How to solve a system of two equations in two unknowns, where one equation is linear and the other is quadratic.

In our discussion of each of these methods, we give the general explanation on the left and an example on the right.

A. How to solve a linear equation in one unknown.

B. How to solve a linear inequality in one unknown.

Note that, in general, there are an infinite number of solutions, although, as in solving a linear equationmethod A a B ovethere will be no solutions if the inequality reduces to 0 x > a where a is positive or to 0 x < a where a is negative.

C. How to use the quadratic formula to solve a quadratic equation in one unknown.

D. How to use factoring to solve a quadratic equation in one unknown.

Note that the method of factoring is usually the simpler way to solve a quadratic equation, provided that you are A B L e to find the factors of ax 2 + bx + c . If you are not A B L e to do so, then you can always rely on the quadratic formula.

E. How to use the substitution method to solve a simultaneous system of two linear equations in two unknowns.

F. How to use the method of elimination to solve a simultaneous system of two linear equations in two unknowns.

It is also possible that we obtain an equation of the form 0 y = 0. In this case, any value of y can be used to obtain a value of x . The equations are said to be dependent and there are infinitely many solutions.

In all other cases the solution is unique.