
Copyright
Copyright 2019 by Boris Pritsker
All rights reserved.
Bibliographical Note
The EquationsWorld is a new work, published first published by Dover Publications, Inc., in 2019.
International Standard Book Number
ISBN-13: 978-0-486-83280-7
ISBN-10: 0-486-83280-5
Manufactured in the United States by LSC Communications
83280501 2019
www.doverpublications.com
Dedication
The Equations World is dedicated to people very close to me, who I love and admire and who had great influence on my life.
To my teachers, former colleagues and close friends at Kiev high school #49; Yarovaya Faina Romanovna, for her friendship and love, encouragement and constant support; and in memory of the late Elgort Leonid Isaakovich and Anisimova Lyudmila Veniominovna.
To my college professor and math scientific advisor at Kiev State Pedagogical University Mikhalin Gennadi Aleksandrovich, who inspired, supported, and guided my first steps in the profession.
To my loving wife Irina, for her understanding, inspiration, sense of humor, and her patience towards my recent book-writing activities.
With great love to my sons Aleksandr and Bryan, whose futures I believe are bright and boundless. Special gratitude goes to Bryan for his help in editing several chapters in the book.
In memory of my beloved parents Polina and Samuil, whose unconditional love, support, and faith in me always helped me in the past and will stay with me for the rest of my life.
Contents
Preface
Equations are more important to me, because politics is for the present, but an equation is something for eternity Albert Einstein

The weight of a cake equals one kilogram and half of the cakes weight. What is its weight? my dad asked me with a smile, expecting a quick response. I was eight or nine years old back then and loved those cute logical puzzles he gave me from time to time. Without hesitation I answered, Its easy. The cakes weight is 1.5 kilograms. (I was born and grew up in Kiev, Ukraine, where metric system measurements were used). Wrong. Think again. It took me a while to finally realize the trick and solve the problem with his help. I have to admit, I admire my dads patience because every time he explained it to me I still was not convinced that my original solution was wrong. OK. Lets try this. Assume you put this cake on one side of a weighing scale and you place half of the same cake and a 1 kilogram weight on the other scale. The weighing scale must be in balance. Then just assume you cut the cake in half and take from each scale half of it. Obviously, the scales will still be in balance. On the left-hand side there is half of a cake and there is a one kilogram weight on the other side. So, what does it mean? This time I gave the correct responsesince half of a cake weighs one kilogram, then the whole cake should weigh 2 kilograms. WOW!!!
That problem is still one of my favorite illustrations of the brilliance of the use of equations in our lives. A weighing scale, balance, or seesaw is often presented as an analogy to an equation. Indeed, if we denote the cakes weight by x, then its easy to set up an obvious equation: 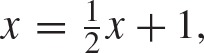 which will result in x = 2. It was one of the first algebra lessons in my life. It was a very convincing example of the importance of equations in problems solutions.
which will result in x = 2. It was one of the first algebra lessons in my life. It was a very convincing example of the importance of equations in problems solutions.
A few years ago I came across one interesting fact about Yuri Gagarins first human flight into outer space. Scientists had no idea how the human body and brain would react to unusual space conditions. Their biggest concern was psychological endurance. They were afraid that the astronaut might lose self-control and become insane and destroy the operational panel. As a precaution a special defense system was created to not allow the astronaut to suppress the automatic operation to manual. In order to switch the space ships pilot program from auto to manual in case of an emergency, Yuri Gagarin would have to open a sealed envelope with a math problem inside. Only after solving the problem would he be able to gain the code for unblocking the operational system from auto to manual. Its hard to imagine a better example of the importance of mathematics in human life!
What science can there be more noble, more excellent, more useful for men, more admirably high and demonstrative, than this of mathematics, said one of the founding fathers of the United States, Benjamin Franklin. Mathematics is the queen of all technical sciences. In todays world, mathematical principles and mathematical modeling are incorporated into almost every aspect of any scientific research. Physics, chemistry, biotechnology, engineering, robotics, statistics, computer science, architecture, geodesy, you name it, cannot survive without the application of mathematics. Equations are the foundation of the great field of mathematics. They are the lifeblood of mathematics, science, and technology. In one way or another you come across setting up and solving equations in many problems.
This book is about equations. It is about various methods and techniques applied in equations solutions. From simple problems involving linear equations to difficult and challenging math contest problems, we will explore the amazing world of variables combined in statements that help make complicated things easy and elegant, and reveal deep and beautiful patterns and regulations. As a matter of fact, equations serve as a universal language for all people no matter what nationality or origin they are.
People invented Esperanto as an international auxiliary language to help communicate in various matters. But there is no need for Esperanto when mathematicians talk with each other using math symbols and equations.
Babylonian mathematicians could solve problems involving calculation of areas and perimeters of rectangles as early as 2000 BC. Mathematicians of Greece, Egypt, India, and China used geometric methods to solve linear and quadratic equations back in 1650 BC. The introduction of the Cartesian coordinate system by the great French mathematician and philosopher Ren Descartes (15961650) provided the link between Euclidean geometry and algebra. The studies of Franois Vite (15401603), Sir Isaac Newton (16421726), Gottfried Wilhelm Leibniz (16461716), Abraham de Moivre (16671754), Leonhard Euler (17071783), Joseph-Louis Lagrange (17361813), Pierre Laurent Wantzel (18141848), Carl Friedrich Gauss (17771855),Augustin-Louis Cauchy (17891857),Niels Henrik Abel (18021829),variste Galois (18111832), and other prominent mathematicians significantly revolutionized and developed algebraic methods that are broadly used today.
The major topics in the book are: linear equations and systems of linear equations, quadratic equations, Vites formulas, application of quadratic function properties in solution of the equations with parameters, cubic and quartic equations, Cardanos formula, Ferraris method, and other techniques for the solutions of cubic and quartic equations, division of polynomials, Little Bezouts Theorem and its applications, irrational equations, exponential and logarithmic equations, trigonometric equations and their applications, conditions for constructability of regular polygons and how they relate to cyclotomic equations, Diophantine and other multivariable equations, systems of nonlinear equations with two or more variables, search for integer solutions with the help of linear homogeneous recurrence relations properties, the Golden Ratio, and the Fibonacci sequence properties. Along with going over some basic fundamental definitions and theorems, we offer a set of non-routine problems that stimulate readers to explore unfamiliar or little-known aspects of mathematics. The main idea is to present an insight into the great field of mathematics by showing diverse problem-solving methods and techniques. The book furnishes a bridge across the mathematical disciplines of algebra, geometry, number theory, and trigonometry. It exposes various equations and systems of equations and covers a wide spectrum of techniques and algorithms for their solutions and applications in more than 280 problems. We restrict our studies mostly to the field of real numbers and try to stay in the boundaries of the high school curriculum. Discussing the history and development of the equations study is impossible without mentioning complex numbers. The introduction and the use of complex numbers in solving algebraic equations was a great revolution. We will be referring to these numbers in several chapters. However, we feel their properties represent more advanced topics. The detailed discussions of complex numbers, therefore, will be omitted, and while solving equations, we will be seeking real, not imaginary, solutions, unless indicated otherwise.












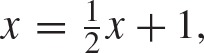 which will result in x = 2. It was one of the first algebra lessons in my life. It was a very convincing example of the importance of equations in problems solutions.
which will result in x = 2. It was one of the first algebra lessons in my life. It was a very convincing example of the importance of equations in problems solutions.