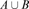A concise yet elementary introduction to measure and integration theory, which are vital in many areas of mathematics, including analysis, probability, mathematical physics and finance. In this highly successful textbook the core ideas of measure and integration are explored, and martingales are used to develop the theory further. Additional topics are also covered such as: Jacobi's transformation theorem; the RadonNikodym theorem; differentiation of measures and HardyLittlewood maximal functions.
In this second edition, readers will find newly added chapters on Hausdorff measures, Fourier analysis, vague convergence, and classical proofs of the RadonNikodym and Riesz representation theorems. All proofs are carefully worked out with utmost clarity to ensure full understanding of the material and its background.
Requiring few prerequisites, this book is a suitable text for undergraduate lecture courses or self-study. Numerous illustrations and over 400 exercises help to consolidate and broaden the reader's knowledge. Full solutions to all exercises are available on the author's webpage at www.motapa.de.
REN L. SCHILLING is a Professor of Mathematics at Technische Universitt, Dresden. His main research area is stochastic analysis and stochastic processes.
Ren L. Schilling
University Printing House, Cambridge CB2 8BS, United Kingdom
One Liberty Plaza, 20th Floor, New York, NY 10006, USA
477 Williamstown Road, Port Melbourne, VIC 3207, Australia
4843/24, 2nd Floor, Ansari Road, Daryaganj, Delhi 110002, India
79 Anson Road, #06-04/06, Singapore 079906
Cambridge University Press is part of the University of Cambridge.
It furthers the University's mission by disseminating knowledge in the pursuit of education, learning, and research at the highest international levels of excellence.
www.cambridge.org
Information on this title: www.cambridge.org/9781316620243
DOI: 10.1017/9781316718339
Ren L. Schilling 2005, 2017
This publication is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press.
First published 2005
Second edition 2017
Printed in the United Kingdom by Clays, St Ives plc
A catalogue record for this publication is available from the British Library.
ISBN 978-1-316-62024-3 Paperback
Cambridge University Press has no responsibility for the presistence or accuracy of URLs for external or third-party Internet Web sites referred to in this publication and does not guarantee that any content on such Web sites is, or will remain, accurate or appropriate.
List of Symbols
This is intended to aid cross-referencing, so notation that is specific to a single section is generally not listed. Some symbols are used locally, without ambiguity, in senses other than those given below. Numbers following entries are page numbers, with the occasional (Pr m.n ) referring to Problem m.n on the respective page.
Unless stated otherwise, binary operations between functions such as fg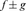 , fg
, fg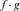 , fg
, fg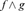 , fg
, fg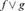 , comparisons fg
, comparisons fg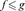 , f or limiting relations fnnf
, f or limiting relations fnnf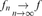 , limnfn
, limnfn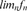 , liminfnfn
, liminfnfn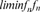 , limsupfn
, limsupfn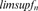 , supifi
, supifi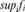 or infifi
or infifi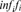 are always understood pointwise.
are always understood pointwise.
Alternatives are indicated by square brackets, i.e., if A [ B ] then P [ Q ] should be read as if A then P and if B then Q .
Generalities positive
always in the sense 0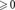
negative
always in the sense 0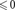

natural numbers: 1,2,3,
0
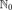
positive integers: 0,1,2,
,,,
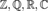
integer, rational, real, complex numbers

[-,+]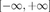
inf,sup
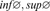
inf=+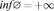 , sup=-
, sup=-
ab
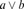
maximum of a and b
ab

minimum of a and b
liminfnan
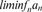
supk infnkan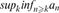 , 409
, 409
limsupnan
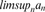
infksupnkan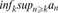 , 409
, 409
|x|
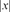
Euclidean norm in n , |x|2=x12++xn2
, |x|2=x12++xn2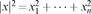
x,y
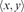
scalar product i=1nxiyi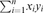
n
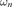
volume of the unit ball in n , 181
, 181
Sets and set operations AB
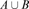







![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)








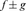 , fg
, fg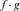 , fg
, fg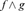 , fg
, fg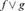 , comparisons fg
, comparisons fg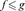 , f or limiting relations fnnf
, f or limiting relations fnnf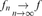 , limnfn
, limnfn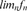 , liminfnfn
, liminfnfn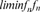 , limsupfn
, limsupfn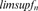 , supifi
, supifi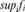 or infifi
or infifi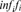 are always understood pointwise.
are always understood pointwise.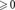
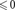

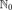
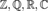

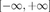
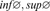
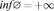 , sup=-
, sup=-
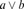

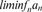
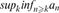 , 409
, 409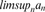
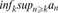 , 409
, 409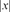
 , |x|2=x12++xn2
, |x|2=x12++xn2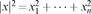
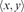
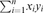
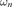
 , 181
, 181