We assume basic knowledge about the numbers that we count with; that is, the numbers 1, 2, 3, 4, 5, 6, and so on. These are called the natural numbers , and the set consisting of all of them is usually denoted by

. They do seem to be very natural, in the sense that they arose very early on in virtually all societies. There are many other names for these numbers, such as the positive integers and the positive whole numbers . Although the natural numbers are very familiar, we will see that they have many interesting properties beyond the obvious ones. Moreover, there are many questions about the natural numbers to which nobody knows the answer. Some of these questions can be stated very simply, as we shall see, although their solution has eluded the thousands of mathematicians who have attempted to solve them.
We assume familiarity with the two basic operations on the natural numbers, addition and multiplication. The sum of two numbers will be indicated using the plus sign +. Multiplication will be indicated by putting a dot in the middle of the line between the numbers, or by simply writing the symbols for the numbers next to each other, or sometimes by enclosing them in parentheses. For example, the product of 3 and 2 could be denoted 3 2 or (3)(2). The product of the natural numbers represented by the symbols m and n could be denoted mn , or m n , or ( m )( n ).
We assume that you know how to add two negative integers and also how to add a negative integer to a positive integer. Multiplication appears to be a bit more mysterious. Most people feel comfortable with the fact that, for m and n natural numbers, the product of m and ( n ) is mn . What some people find more mysterious is the fact that
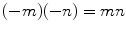
for natural numbers m and n ; that is, the product of two negative integers is a positive integer. There are various possible explanations that can be provided for this, one of which is the following. Using the usual rules of arithmetic:
Adding mn to both sides of this equation gives
or
Thus,
so,
Therefore, the fact that
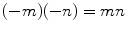
is implied by the other standard rules of arithmetic.
1.1 Prime Numbers
One of the important concepts we will study is divisibility . For example, 12 is divisible by 3, which means that there is a natural number (in this case, 4) such that the product of 3 and that natural number is 12. That is, 12=3 4. In general, we say that the integer m is divisible by the integer n if there is an integer q such that m = nq . There are many other terms that are used to describe such a relationship. For example, if m = nq , we may say that n and q are divisors of m and that each of n and q divides m . The terminology q is the quotient when m is divided by n is also used when n is different from 0. In this situation, n and q are also sometimes called factors of m ; the process of writing an integer as a product of two or more integers is called factoring the integer.
The number 1 is a divisor of every natural number since, for each natural number m , m =1 m . Also, every natural number m is a divisor of itself, since m = m 1.
The number 1 is the only natural number that has only one natural number divisor, namely itself. Every other natural number has at least two divisors, itself and 1. The natural numbers that have exactly two natural number divisors are called prime numbers . That is, a prime number is a natural number greater than 1 whose only natural number divisors are 1 and the number itself. We do not consider the number 1 to be a prime; the first prime number is 2. The primes continue: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and so on.
And so on? Is there a largest prime? Or does the sequence of primes continue without end? There is, of course, no largest natural number. For if n is any natural number, then n + 1 is a natural number and n + 1 is bigger than n . It is not so easy to determine if there is a largest prime number or not. If p is a prime, then p + 1 is almost never a prime. Of course, if p =2, then
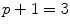
and p and p + 1 are both primes. However, 2 is the only prime number p for which p + 1 is prime. This can be proven as follows. First note that, since every even number is divisible by 2, 2 itself is the only even prime number. Therefore, if p is a prime other than 2, then p is odd and p + 1 is an even number larger than 2 and is thus not prime.
Is it nonetheless true that, given any prime number p , there is a prime number larger than p ? Although we cannot get a larger prime by simply adding 1 to a given prime, there may be some other way of producing a prime larger than any given one. We will answer this question after learning a little more about primes.
A natural number, other than 1, that is not prime is said to be composite . (The number 1 is special and is neither prime nor composite.) For example, 4, 68, 129, and 2010 are composites. Thus, a composite number is a natural number other than 1 that has a divisor in addition to itself and 1.
To determine if a number is prime, what potential factors must be checked to eliminate the possibility that there are factors other than the number and 1? If m = n q , it is not possible that n and q are both larger than the square root of m , for if two natural numbers are both larger than the square root of m , then their product is larger than m . It follows that a natural number (other than 1) that is not prime has at least one divisor that is larger than 1 and is no larger than the square root of that natural number. Thus, to check whether or not a natural number m is prime, you need not check whether every natural number less than m divides m . It suffices to check if m has a divisor that is larger than 1 and no larger than the square root of m . If it has such a divisor, it is composite; if it has no such divisor, it is prime.










 . They do seem to be very natural, in the sense that they arose very early on in virtually all societies. There are many other names for these numbers, such as the positive integers and the positive whole numbers . Although the natural numbers are very familiar, we will see that they have many interesting properties beyond the obvious ones. Moreover, there are many questions about the natural numbers to which nobody knows the answer. Some of these questions can be stated very simply, as we shall see, although their solution has eluded the thousands of mathematicians who have attempted to solve them.
. They do seem to be very natural, in the sense that they arose very early on in virtually all societies. There are many other names for these numbers, such as the positive integers and the positive whole numbers . Although the natural numbers are very familiar, we will see that they have many interesting properties beyond the obvious ones. Moreover, there are many questions about the natural numbers to which nobody knows the answer. Some of these questions can be stated very simply, as we shall see, although their solution has eluded the thousands of mathematicians who have attempted to solve them.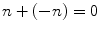 . Altogether, the collection of positive and negative numbers and 0 is called the integers . It is often denoted by
. Altogether, the collection of positive and negative numbers and 0 is called the integers . It is often denoted by 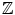 .
.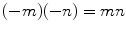 for natural numbers m and n ; that is, the product of two negative integers is a positive integer. There are various possible explanations that can be provided for this, one of which is the following. Using the usual rules of arithmetic:
for natural numbers m and n ; that is, the product of two negative integers is a positive integer. There are various possible explanations that can be provided for this, one of which is the following. Using the usual rules of arithmetic: 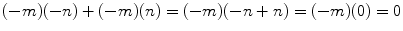
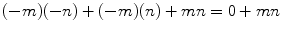
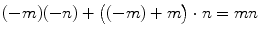
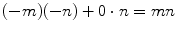
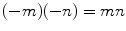
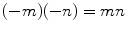 is implied by the other standard rules of arithmetic.
is implied by the other standard rules of arithmetic.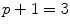 and p and p + 1 are both primes. However, 2 is the only prime number p for which p + 1 is prime. This can be proven as follows. First note that, since every even number is divisible by 2, 2 itself is the only even prime number. Therefore, if p is a prime other than 2, then p is odd and p + 1 is an even number larger than 2 and is thus not prime.
and p and p + 1 are both primes. However, 2 is the only prime number p for which p + 1 is prime. This can be proven as follows. First note that, since every even number is divisible by 2, 2 itself is the only even prime number. Therefore, if p is a prime other than 2, then p is odd and p + 1 is an even number larger than 2 and is thus not prime.