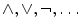Rautenberg - A concise introduction to mathematical logic
Here you can read online Rautenberg - A concise introduction to mathematical logic full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: New York, year: 2010, publisher: Springer, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:A concise introduction to mathematical logic
- Author:
- Publisher:Springer
- Genre:
- Year:2010
- City:New York
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
A concise introduction to mathematical logic: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "A concise introduction to mathematical logic" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Traditional logic as a part of philosophy is one of the oldest scientific disciplines and can be traced back to the Stoics and to Aristotle. Mathematical logic, however, is a relatively young discipline and arose from the endeavors of Peano, Frege, and others to create a logistic foundation for mathematics. It steadily developed during the twentieth century into a broad discipline with several sub-areas and numerous applications in mathematics, informatics, linguistics and philosophy.
This book treats the most important material in a concise and streamlined fashion. The third edition is a thorough and expanded revision of the former. Although the book is intended for use as a graduate text, the first three chapters can easily be read by undergraduates interested in mathematical logic. These initial chapters cover the material for an introductory course on mathematical logic, combined with applications of formalization techniques to set theory. Chapter 3 is partly of descriptive nature, providing a view towards algorithmic decision problems, automated theorem proving, non-standard models including non-standard analysis, and related topics.
The remaining chapters contain basic material on logic programming for logicians and computer scientists, model theory, recursion theory, Gdels Incompleteness Theorems, and applications of mathematical logic. Philosophical and foundational problems of mathematics are discussed throughout the text. Each section of the seven chapters ends with exercises some of which of importance for the text itself. There are hints to most of the exercises in a separate file Solution Hints to the Exercises which is not part of the book but is available from the authors website.
Rautenberg: author's other books
Who wrote A concise introduction to mathematical logic? Find out the surname, the name of the author of the book and a list of all author's works by series.












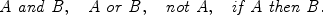
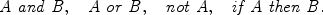
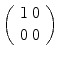 , where, in general,
, where, in general, 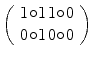 represents the value matrix or truth table of a binary function with arguments and values in {0, 1}. The delimiters of these small matrices will usually be omitted.
represents the value matrix or truth table of a binary function with arguments and values in {0, 1}. The delimiters of these small matrices will usually be omitted.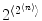 . We denote their totality by Bn . While B 2 has 24 = 16 members, there are only four unary Boolean functions. One of these is negation , denoted by and defined by 1 = 0 and 0 = 1. B 0 consists just of the constants 0 and 1.
. We denote their totality by Bn . While B 2 has 24 = 16 members, there are only four unary Boolean functions. One of these is negation , denoted by and defined by 1 = 0 and 0 = 1. B 0 consists just of the constants 0 and 1.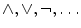 themselves, setting their meaning temporarily aside. Then we talk of the connectives or truth functors
themselves, setting their meaning temporarily aside. Then we talk of the connectives or truth functors