The main objects of study in mathematical logic are mathematical theories such as set theory, number theory, and the theory of algebraic structures such as groups, rings, fields, algebraically closed fields, etc., with the aim of developing tools to examine their consistency, completeness, and other similar questions concerning the foundation of these theories. In this chapter we take the first step toward logic and precisely define the notion of a first-order theory.
1.1 First-Order Languages
The objects of study in the natural sciences have a physical existence. By contrast, mathematical objects are concepts, e.g., sets, belongs to (), natural numbers, real numbers, complex numbers, lines, curves, addition, multiplication, etc.
There must be initial concepts in a theory. To elaborate on this a bit more, note that a concept can be defined in terms of other concepts. For instance, x y is the unique number z such that
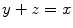
; or if x and y are sets, x y if for every element z , z x implies z y . Thus, subtraction can be defined in terms of addition and subset () in terms of belongs to (). At the onset, one begins with a minimal number of undefined concepts. For instance, in set theory, the undefined concepts are sets and belongs to; in number theory, the undefined concepts are natural numbers, zero, and the successor function; in the theory of real numbers (seen as an archimedean ordered field), the undefined concepts are real numbers, zero, one, addition, multiplication, and less than. In these examples, we see that there are two groups of concepts: sets or natural numbers or real numbers on the one hand and belongs to, zero, one, successor, addition, multiplication, less than, etc. on the other. Concepts of the first type are the main objects of study; concepts of the second type are used to reflect basic structural properties of the objects of the first type. Then one lists a set of axioms that give the basic structural properties of the objects of study. It is expected that based on these undefined concepts and on the axioms, other concepts can be defined. Then the theory is developed by introducing more and more concepts and proving more and more theorems.
Clearly, we ought to have a language to develop a theory. Like any of the natural languages, for example, Latin, Sanskrit, or Tamil, a language suitable for a mathematical theory also has an alphabet. But unlike natural languages, a statement in a mathematical theory is expressed symbolically and has an unambiguous syntactical construction. Before giving precise definitions, we give some examples of statements in some theories that we are familiar with.
Example 1.1.1.
Consider the following statement in group theory. For every x there exists y such that x y = e . Here (dot) is a symbol for the binary group operation and e for the identity element. If we use the symbol
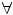
to denote for every and for there exists, then we can represent the foregoing statement as follows:
Example 1.1.2.
The following two statements appear in set theory:
and
The first statement is a symbolic representation of the statement Given any two sets x and y , there is a set z that contains both x and y ; the second statement means There is no set x that contains all sets y .
We see that the language for a theory should have variables to represent the objects of study, e.g., sets in set theory, or elements of a group in group theory, etc., and some logical symbols like (there exists),(and), (negation),=(equality). These symbols are common to the languages for all theories. We call them logical symbols. On the other hand, there are certain alphabets that represent undefined concepts of a specific theory. For instance, in group theory we use two symbols: the dot for the group operation and a symbol, say e , for the identity element; in set theory we have a binary relation symbolfor the undefined concept belongs to.
We make one more observation before giving the first definition in the subject. Mathematicians use many logical connectives and quantifiers such as(or),(and), (there exists),
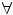
(for all),(if , then ), and(if and only if). However, in their reasoning two statements A and B are both true if and only if it is not true that any of A or B is false; A implies B if and only if either A is false or B is true, etc. This indicates that some of the logical connectives and quantifiers can be defined in terms of others. Thus, we can start with a few logical connectives and quantifiers. This economy will help in making many proofs quite short.
A first-order languageL consists of two types of symbols: logical symbols and nonlogical symbols . Logical symbols consist of a sequence of variablesx 0, x 1, x 2,; logical connectives (negation) and(disjunction); a logical quantifier (existential quantifier); and the equality symbol =. We call the order in which variables x 0, x 1, x 2, are listed the alphabetical order . These are common to all first-order languages. Depending on the theory, nonlogical symbols of L consist of an (empty or nonempty) set of constant symbols { c i : i I }; for each positive integer n , a set of n -ary function symbols { f j : j J n }; and a set of n -ary relation symbols { p k : k K n }.
When it is clear from the context, a first-order language will simply be called a language. Since logical symbols are the same for all languages, to specify a language one must specify its nonlogical symbols only. The collection of all nonlogical symbols is sometimes called the signature of the language. To avoid suffixes and for ease in reading, we shall use symbols x , y , z , u , v , w , with or without subscripts, to denote variables. Any finite sequence of symbols of a language L will be called an expression in L .
A language L is called countable if it has only countably many nonlogical symbols; it is called finite if it has finitely many nonlogical symbols.
Example 1.1.3.
The language for set theory has only one nonlogical symbol: a binary relation symbolfor belongs to.
Example 1.1.4.
The language for group theory has a constant symbol e (for the identity element) and a binary function symbol (for the group operation).














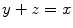 ; or if x and y are sets, x y if for every element z , z x implies z y . Thus, subtraction can be defined in terms of addition and subset () in terms of belongs to (). At the onset, one begins with a minimal number of undefined concepts. For instance, in set theory, the undefined concepts are sets and belongs to; in number theory, the undefined concepts are natural numbers, zero, and the successor function; in the theory of real numbers (seen as an archimedean ordered field), the undefined concepts are real numbers, zero, one, addition, multiplication, and less than. In these examples, we see that there are two groups of concepts: sets or natural numbers or real numbers on the one hand and belongs to, zero, one, successor, addition, multiplication, less than, etc. on the other. Concepts of the first type are the main objects of study; concepts of the second type are used to reflect basic structural properties of the objects of the first type. Then one lists a set of axioms that give the basic structural properties of the objects of study. It is expected that based on these undefined concepts and on the axioms, other concepts can be defined. Then the theory is developed by introducing more and more concepts and proving more and more theorems.
; or if x and y are sets, x y if for every element z , z x implies z y . Thus, subtraction can be defined in terms of addition and subset () in terms of belongs to (). At the onset, one begins with a minimal number of undefined concepts. For instance, in set theory, the undefined concepts are sets and belongs to; in number theory, the undefined concepts are natural numbers, zero, and the successor function; in the theory of real numbers (seen as an archimedean ordered field), the undefined concepts are real numbers, zero, one, addition, multiplication, and less than. In these examples, we see that there are two groups of concepts: sets or natural numbers or real numbers on the one hand and belongs to, zero, one, successor, addition, multiplication, less than, etc. on the other. Concepts of the first type are the main objects of study; concepts of the second type are used to reflect basic structural properties of the objects of the first type. Then one lists a set of axioms that give the basic structural properties of the objects of study. It is expected that based on these undefined concepts and on the axioms, other concepts can be defined. Then the theory is developed by introducing more and more concepts and proving more and more theorems.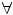 to denote for every and for there exists, then we can represent the foregoing statement as follows:
to denote for every and for there exists, then we can represent the foregoing statement as follows: 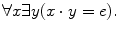
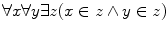
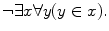
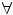 (for all),(if , then ), and(if and only if). However, in their reasoning two statements A and B are both true if and only if it is not true that any of A or B is false; A implies B if and only if either A is false or B is true, etc. This indicates that some of the logical connectives and quantifiers can be defined in terms of others. Thus, we can start with a few logical connectives and quantifiers. This economy will help in making many proofs quite short.
(for all),(if , then ), and(if and only if). However, in their reasoning two statements A and B are both true if and only if it is not true that any of A or B is false; A implies B if and only if either A is false or B is true, etc. This indicates that some of the logical connectives and quantifiers can be defined in terms of others. Thus, we can start with a few logical connectives and quantifiers. This economy will help in making many proofs quite short.