György E. Révész - Introduction to Formal Languages

Gyrgy E. Rvsz

Professor Emeritus of Computer Science

University of North Carolina at Charlotte

Dover Publications, Inc.,
Mineola, New York

TO MY SONS,
Szilrd, Tams, and Peter

Copyright 1983 by Gyrgy E. Rvsz. All rights reserved.

This Dover edition, first published in 1991, and reissued in 2012, is an unabridged and slightly corrected republicaiton of the work first published by the McGraw-Hill Book Company, New York, in 1983 in the McGraw-Hill Computer Science Series.

Library of Congress Cataloging-in-Publication Data

Rvsz, Gyrgy E.

Introduction to formal languages / Gyrgy E. Rvsz.

p. cm.

Unabridged and slightly corrected republication of the work first published by the McGraw-Hill Book Company in 1983 in the McGraw-Hill computer science seriesT.p. verso.

Includes bibliographical references and index.

ISBN 13: 978-0-486-66697-6 (pbk.)

ISBN 10: 0-486-66697-2 (pbk.)

1. Formal languages. I. Title.

QA267.3.R485 1991

511.3dc20

91-11606

CIP

Manufactured in the United States by Courier Corporation
66697204
www.doverpublications.com

Formal languages have been playing a fundamental role in the progress of computer science. Formal notations in mathematics, logic, and other sciences had been developed long before the advent of electronic computers. The evolution of formal notations was slow enough to allow the selection of those patterns which appeared to be the most favorable for their users, but the computer revolution has resulted in an unprecedented proliferation of artificial languages. Given time, I presume, natural selection would take effect, but for now we have to face this modern story of the Tower of Babel.

The purpose of a scientific theory is to bring order to the chaos, and this is what formal language theory is trying to dowith partial success. Unfortunately, the theory itself sometimes appears to be in serious disorder, and nobody knows for sure which way it will turn next time. One important feature, however, is apparent so far: there is a close relationship between formal grammars and other abstract notions used in computer science, such as automata and algorithms. Indeed, since the results in one theory can often be translated into another, it seems to be an arbitrary decision as to which interpretation is primary.

In this book, formal grammars are given preferential treatment because they are probably the most commonly known of the various theories among computer scientists. This is due to the success of context-free grammars in describing the syntax of programming languages. For this reason, I have also changed the proofs of some of the classical theorems which are). In this way, the introduction of the latter notion is deferred until it really becomes necessary; at the same time a more uniform treatment of the subject is presented. The connection between grammars and automata is also emphasized by the similarity of the notation for derivation and reduction, respectively.

. His enthusiasm and encouragement with respect to the writing of the entire book is greatly appreciated.

Chapters 1 through 9 can be used as the primary text for graduate or senior undergraduate courses in formal language theory. Automata theory and complexity theory are not studied here in depth. Nevertheless, the text provides sufficient background in those areas that they can be explored more specifically in other courses later on. The same is true for computability theory, that is, the theory of algorithms. In the areas of compiler design and programming language semantics, I feel that my book can have a favorable influence on the way of thinking about these subjects, though less directly.

Some of the theorems, e.g., without proofs except in a very few cases.

Gyrgy Rvsz

A finite nonvoid set of arbitrary symbols (such as the letters used for writing in some natural language or the characters available on the keyboard of a typewriter) is called a finite alphabet and will usually be denoted by V . The elements of V are called letters or symbols and the finite strings of letters are called words over V . The set of all words over V is denoted by V *. The empty word , which contains no letters, will be denoted by and is considered to be in V * for every V .

Two words written in one is called the catenation of the given words. The catenation of words is an associative operation, but in general it is noncommutative. Thus, if P and Q are in V * then their catenation PQ is usually different from QP except when V contains only one letter. But for every P , Q , and R in V * the catenation of PQ and R is the same as the catenation of P and QR . Therefore, the resulting word can be written as PQR without parentheses. The set V * is obviously closed with respect to catenation, that is, the result PQ is always in V * whenever both P and Q are in V . The empty word plays the role of the unit element for catenation, namely P = P = P for every P . (We shall assume that P is in V * for some given V even if we do not mention that.)

The length of P denoted by | P | is simply the number of letters of P . Hence || = 0 and | PQ | = | P | + | Q | for every P and Q . Two words are equal if one is a letter by letter copy of the other. The word P is a part of Q if there are words P and P such that Q = P PP . Further, if P and P Q , then it is a proper part of Q and if P = or P = then P is a head (initial part) or a tail of Q , respectively.

For a positive integer i and for an arbitrary word P we denote by P i the i-times iterated catenation of P (that is, i copies of P written in one word). By convention P = for every P . If, for example, P = ab , then P = ababab . (Note that we need parentheses to distinguish ( ab ) = ababab from ab = abbb .)

The mirror image of P , denoted by P , is the word obtained by writing the letters of P in the reverse order. Thus, if P = a a a n then P = a n a n 1 a . Clearly, ( P ) = P and ( P ) i = ( P i ) for i = 0, 1,.

An arbitrary set of words of V * is called a language and is usually denoted by L . The empty language containing no words at all is denoted by . It should not be confused with the language {} containing a single word . The set V * without is denoted by V + . A language L V * is finite if it contains a finite number of words, otherwise it is infinite. The complete language V * is always denumerably infinite. (The set of all subsets of V* , that is, the set of languages over a finite alphabet, is nondenumerable.)

The above notion of language is fairly general but not extremely practical. It includes all written natural languages as well as the artificial ones, but it does not tell us how to define a particular language. Naturally, we want finiteand possibly concisedescriptions for the mostly infinite languages we are dealing with. In some cases we may have a finite characterization via some simple property. If, for instance, V = { a , b } then

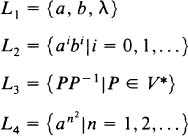
are all well-defined languages. Or let N a ( P ) and N b ( P ) denote the number of occurrences of a and b , respectively, in P . Then

L = { P | P { a , b } + and N a ( P ) = N b ( P )}

is also well-defined. But we need other, more specific tools to define more realistic languages. For this purpose the notion of generative grammar will be introduced as follows:

Definition 1.1 A generative grammar G is an ordered fourtuple ( V N , V T , S , F ) where V N and V T are finite alphabets with V N V T = , S is a distinguished symbol of V N , and F is a finite set of ordered pairs ( P , Q ) such that P and Q are in ( V N V T )* and P contains at least one symbol from V N .