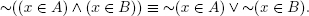Contents
Pagebreaks of the print version

A BEGINNERS FURTHER GUIDE
TO MATHEMATICAL LOGIC

A BEGINNERS FURTHER GUIDE
TO MATHEMATICAL LOGIC
Raymond Smullyan

Published by
World Scientific Publishing Co. Pte. Ltd.
5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
Library of Congress Cataloging-in-Publication Data
Names: Smullyan, Raymond M., author.
Title: A beginners further guide to mathematical logic / Raymond Smullyan.
Description: New Jersey : World Scientific, 2016. | Includes bibliographical references and index.
Identifiers: LCCN 2015033651 | ISBN 9789814730990 (hardcover : alk. paper) | ISBN 9789814725729 (pbk : alk. paper)
Subjects: LCSH: Logic, Symbolic and mathematical.
Classification: LCC QA9.A1 S619 2016 | DDC 511.3--dc23
LC record available at http://lccn.loc.gov/2015033651
British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library.
On the cover, the three photos from left to right are the logicians
Emil Post, Alan Turing, and Ernst Zermelo.
Copyright 2017 by World Scientific Publishing Co. Pte. Ltd.
All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher.
For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.
Typeset by Stallion Press
Email:
Printed in Singapore
Contents
Preface
This book is a sequel to my Beginners Guide to Mathematical Logic [Smullyan, 2014]. I originally intended both volumes to be a single volume, but I felt that at my age (now 96), I could pass away at any time, and I wanted to be sure that I would at least get the basic material out.
The previous volume deals with elements of propositional and first-order logic, contains a bit on formal systems and recursion, and concludes with chapters on Gdels famous incompleteness theorem, along with related results.
The present volume begins with a bit more on propositional and first order logic, followed by what I would call a fein chapter, which simultaneously generalizes some results from recursion theory, first-order arithmetic systems, and what I dub a decision machine. Then come four chapters on formal systems, recursion theory and metamathematical applications in a general setting. The concluding five chapters are on the beautiful subject of combinatory logic, which is not only intriguing in its own right, but has important applications to computer science. Argonne National Laboratory is especially involved in these applications, and I am proud to say that its members have found use for some of my results in combinatory logic.
This book does not cover such important subjects as set theory, model theory, proof theory, and modern developments in recursion theory, but the reader, after studying this volume, will be amply prepared for the study of these more advanced topics.
Although this book is written for beginners, there are two chapters namely 3 and 8 that I believe would also be of interest to the expert.
For brevity, all references to the first volume, The Beginners Guide to Mathematical Logic, of this two-volume introduction to mathematical logic will be given in the remainder of this volume as The Beginners Guide [Smullyan, 2014].
Elka Park
November 2016
Part I
More on Propositional and First-Order Logic
Chapter 1
More on Propositional Logic
I.Propositional Logic and the Boolean Algebra of Sets
Many of you have probably noticed the similarity of the logical connectives to the Boolean operations on sets. Indeed, for any two sets A and B and any element x, the element x belongs to the intersection A B if and only if x is in A and x is in B. Thus x (AB) iff (xA) (xB). Thus the logical connective (conjunction) corresponds to the Boolean operation (intersection). Likewise the logical connective (disjunction) corresponds to the Boolean operation (union), since x (AB) iff (xA) (xB) Also, x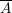 (x is in the complement of A) if and only if (xA) (x is not in A), so that the logical connective negation corresponds to Boolean operation of complementation.
(x is in the complement of A) if and only if (xA) (x is not in A), so that the logical connective negation corresponds to Boolean operation of complementation.
Note: As in The Beginners Guide [Smullyan, 2014], I will often abbreviate the phrase if and only if by iff, following the valuable suggestion of Paul Halmos.
We saw in of The Beginners Guide how to verify the correctness of a Boolean equation by the method of what I called indexing. However, due to the correspondence between the logical connectives and the Boolean operations on sets, one can also verify Boolean equations by truth tables. The following single example will illustrate the general idea. Consider the Boolean equation 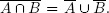 This equation is valid iff for every element x, the element x is in
This equation is valid iff for every element x, the element x is in  iff x is in
iff x is in 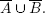 Thus the equation
Thus the equation 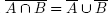 is to the effect that for all x,
is to the effect that for all x,

Thus the proposition x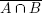 iff x
iff x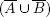 is equivalent to
is equivalent to
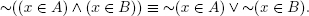
And that formula is a tautology, for it is an instance of (

















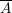 (x is in the complement of A) if and only if (xA) (x is not in A), so that the logical connective negation corresponds to Boolean operation of complementation.
(x is in the complement of A) if and only if (xA) (x is not in A), so that the logical connective negation corresponds to Boolean operation of complementation.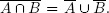 This equation is valid iff for every element x, the element x is in
This equation is valid iff for every element x, the element x is in  iff x is in
iff x is in 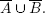 Thus the equation
Thus the equation 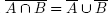 is to the effect that for all x,
is to the effect that for all x,
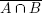 iff x
iff x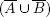 is equivalent to
is equivalent to