Bibliographical Note
This Dover edition, first published in 2011, is an unabridged republication of the work originally published in 1959 by the McGraw-Hill Book Company, Inc., New York.
Library of Congress Cataloging-in-Publication Data
Exner, Robert M.
Logic in elementary mathematics / Robert M. Exner and Myron F. Rosskopf
p. cm.
Originally published: New York : McGraw-Hill, 1959.
Summary: This accessible, applications-related introductory treatment explores some of the structure of modern symbolic logic useful in the exposition of elementary mathematics. Topics include axiomatic structure and the relation of theory to interpretation. No prior training in logic is necessary and numerous examples and exercises aid in the mastery of the language of logic. 1959 editionProvided by publisher.
Includes index.
ISBN-13: 978-0-486-48221-7 (pbk.)
ISBN-10: 0-486-48221-9 (pbk.)
1. MathematicsPhilosophy. 2. Logic, Symbolic and mathematical. I. Rosskopf, Myron Frederick. II. Title.
QA9.E96 2011
510.1dc22
2010052658
Manufactured in the United States by Courier Corporation
48221901
www.doverpublications.com
The threefold purpose of the present text is:
1. To present some of the structure of modern symbolic logic that is useful in the exposition of elementary mathematics.
2. To use the logic in discussion of formal aspects of elementary mathematics.
3. To present the material in such a way that it will be accessible to those whose mathematical training includes the standard elementary courses, but who may lack any formal courses in logic.
It is not our primary interest to develop the logic for its own sake, but rather as a language for discoursing about mathematics. We do not attempt an abstract development of logic from axioms. To justify the logical principles assumed, we lean heavily on the intended interpretation of the logic in mathematics. All mathematical interpretations are elementary in nature. Exercises and examples are included in appropriate places as an aid to mastery of the logical language, and those that are mathematical are drawn from elementary algebra and geometry and trigonometry.
We limit ourselves generally to certain formal and structural aspects of mathematics. It is true that in the first chapter, to highlight our aims by contrast, we do talk about problem solving, mathematical intuition, and the creative side of mathematics. We shall have little further to say, however, about these important matters in succeeding sections, but shall have much to say about the axiomatic structure of mathematics, about proof or demonstration , about the relation of theory to interpretation , about variables, equality , and functions , and other such notions of a formal nature. The notions treated are just those that, in our experience, are most often treated fuzzily in traditional exposition. Indeed, some of the notions we shall treat are entirely tacit in traditional exposition.
The authors owe much to their colleagues and students. The exposition, including exercises, was tested upon both. We owe a greater debt to the mathematicians and logicians whose results we use, and whose clarity of exposition we hope to have approximated. Some of those whose writings have been most helpful are W. Ackermann, Alonzo Church, Irving M. Copi, D. Hilbert, Stephen C. Kleene, Hugues Le Blanc, Willard Van Orman Quine, J. Barkley Rosser, and Alfred Tarski.
Robert M. Exner
Associate Professor of Mathematics
Syracuse University
Myron F. Rosskopf
Professor of Mathematics
Teachers College
Columbia University
CONTENTS
|

| |
& | |
|
|
|
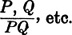
| |
mod pon, m.p. | |
conj inf | |
simp; conj simp | |
hyp syll | |
contrapos inf | |
| |
|
ded prin | |
H ( ), F ( ), etc. | |
( x ); ( x ) | |
( x ) | |
IU | |
PGU* | |
IE | |
PGE | |
PGU | |
R | |
IS | |
F*( y ) | |
ISC | |
e | |
o | |
x 1 | |
1-1 | |
|
F [mod p ] | |
disch assump | 223 (see 178, 180) |

| |
| a | | |
An , { An } | |
contra | |
subst VSF | |
quant conv | 247 (see 138) |
The number opposite each symbol indicates the page on which it is explained.
| MATHEMATICS,
FORMAL LOGIC,
AND NAMES |
That mathematics is one of the oldest and richest of the disciplines is generally conceded. What is not so commonly understood is that mathematics is also one of the most rapidly expanding of the disciplines. Several times in the life of a mathematician he can expect to be asked, But what do you do? Is there anything new to do in mathematics? Scientists and engineers are less subject to this sort of question, for everyone knows that these men are plunging ahead to marvelous new discoveries in their fields. But there is a widespread feeling that mathematics is a precise but static body of knowledge that was pretty well roughed out by the Greeks and other early peoples, leaving little for modern man to do but polish and refine.
Nevertheless, a mathematician finds it much easier to describe what he does than to answer the question What is mathematics? Attempts to define mathematics range from pithy sentences to books in multiple volumes. It has been variously described as a language, a method, a state of mind, a body of abstract relations, and so on. A thoroughly satisfactory definition is not easily attained.
In describing what he does, a mathematician is likely to list creation of new mathematics as one of his important activities. Creation of new mathematics involves first discovering new mathematical relationships and then proving them. In searching for new mathematics, the mathematician does not limit his methods. He uses his imagination and ingenuity to the utmost. He experiments and he guesses. He uses analogies. He may build machines and physical models. He makes some use of deductive methods but much more use of inductive methods. In the heat of the search nothing is illegal.
Once he has guessed a new relationship and has satisfied his intuitions that the new idea is reasonable, the mathematician has what he calls a conjecture . He next tries to change the conjecture into a theorem by proving (or disproving) that the conjecture follows logically from the assumptions and proved theorems of known mathematics. In constructing a proof, he sharply limits himself to the methods of deductive logic. He does not allow his proof to depend on experiment, intuition, or analogy. He tries to present an argument satisfying a set of rules that mathematicians have agreed such arguments must satisfy.