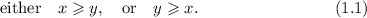Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. OPTIMIZATION THEORYA Concise Introduction Copyright 2018 by World Scientific Publishing Co. Ltd. All rights reserved. All rights reserved.
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. OPTIMIZATION THEORYA Concise Introduction Copyright 2018 by World Scientific Publishing Co. Ltd. All rights reserved. All rights reserved.
This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. ISBN 978-981-3237-64-3 For any available supplementary material, please visit
http://www.worldscientific.com/worldscibooks/10.1142/10923#t=suppl Printed in Singapore To
Meifen and Our Kids
Preface
In daily life, people frequently face problems on decision-making. Among all possible decisions, it is desired to select the best one. Is there the best (or optimal) decision? If yes, how can one find it (efficiently)? Optimization theory is to answer such kinds of questions to some extent. Mathematically, the problem can be formulated as follows.
For a given objective function defined on the set of all decision variables, find a decision such that the objective is optimized (minimized or maximized). As a matter of fact, minimization and maximization problems were one of the main motivations for the invention of calculus back in the 17th century. Subject-wise, optimization theory can actually be regarded as a natural continuation of (advanced) calculus. Needless to say, having some basic knowledge of optimization theory will probably enable people to wisely handle various encountered decision-making problems. On the other hand, except those researchers in the area of optimization theory, most people might only be interested in knowing some basics of optimization theory. Therefore, it should be ideal to have a one-semester course that could cover some basic topics in optimization, including linear, convex, and nonlinear optimization.
This is my motivation of writing this book to meet such a need. In the past few years, I have taught such a course at University of Central Florida several times, in two different levels, for the upper level undergraduate students and first or second year graduate students. This book is based on my lecture notes of the course that I had taught. This book is intended to present a brief introduction to optimization theory. After recalling some basic knowledge of advanced calculus and linear algebra, we start the presentation of general optimization problems, followed by abstract Weierstrass type existence theorems. Then we introduce the Lagrange multiplier method for optimization problems with equality constraints in high dimensions (two- and three-dimensional versions of which are introduced in the standard calculus courses).
After that, KarushKuhnTucker method for problems with equality and inequality constraints is presented. In the case that no regularity condition for the constraints is assumed, we present Fritz Johns necessary conditions for optimal solutions, with the proof by using Ekelands variational principle (such a method has been used in establishing Pontryagins maximum principle in optimal control theory, and to my best knowledge, this method has not been used in the context similar to this book). Next, we present optimization problems under convex/quasi-convex constraints. Some basic important results in convex analysis are presented, such as Carathodory theorem of convex hull representation, separation theorem of convex sets, Lipschitz continuity of convex functions, sufficiency of the KarushKuhnTucker conditions for the problems under convex/quasi-convex constraints, Lagrange duality, and so on. Finally, we present a self-contained theory of linear programming. Characterization of extreme points for the feasible set is presented, weak and strong versions of fundamental theorem of linear programming are established.
Simplex method, including phase I and phase II, as well as sensitivity analysis, and duality theory are presented. The book is designed to be suitable for a one-semester course either for upper level undergraduate students, or first/second year graduate students. For the former, the instructor is recommended to concentrate on the computational/calculative aspect of the material, and skip most proofs of theorems. For the latter, the instructor is suggested to spend less time on the computational aspect, very briefly mention the results from the first chapter, and concentrate on most, if not all, proofs of the theorems.
| Orlando, FL | Jiongmin Yong |
| January 2018 |
Contents
Chapter 1
Mathematical Preparations
In this chapter, we will briefly present some basic results of advanced calculus (analysis) and linear algebra, which will be used in the later chapters. We will mainly concentrate on the definitions and statements of relevant results, with short proofs.
Lengthy proofs will be omitted, and they can be found in standard textbooks of analysis and linear algebra. Also, we do not try to be exhaustive. There are two types of readers that can skip this chapter: Those who have solid knowledge of analysis and linear algebra, and those who are only interested in computational aspects of optimization theory.
1Basics in R n
Let R be the sets of all real numbers. For any
n 1, we define
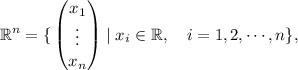
and identify R 1 = R . Elements in R n are called
vectors and briefly denoted by
x,
y,
z, etc., i.e.,
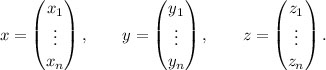
For notational convenience and presentation consistency, we will let all vectors in R n be
column vectors, and denote
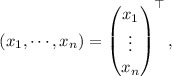
and call it a
row vector, with the superscript being called the
transpose.
Now, let us introduce some binary relations between two vectors. For any x (x1,  , xn), y (y1,
, xn), y (y1,  , yn) R n, we write
, yn) R n, we write 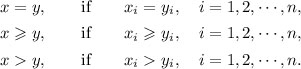 Note that when n = 1, for any x, y R , one must have
Note that when n = 1, for any x, y R , one must have 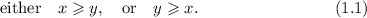
Next page








 Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. OPTIMIZATION THEORYA Concise Introduction Copyright 2018 by World Scientific Publishing Co. Ltd. All rights reserved. All rights reserved.
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. OPTIMIZATION THEORYA Concise Introduction Copyright 2018 by World Scientific Publishing Co. Ltd. All rights reserved. All rights reserved.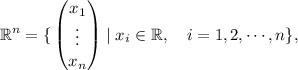 and identify R 1 = R . Elements in R n are called vectors and briefly denoted by x, y, z, etc., i.e.,
and identify R 1 = R . Elements in R n are called vectors and briefly denoted by x, y, z, etc., i.e., 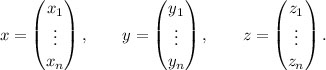 For notational convenience and presentation consistency, we will let all vectors in R n be column vectors, and denote
For notational convenience and presentation consistency, we will let all vectors in R n be column vectors, and denote 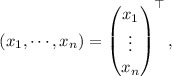 and call it a row vector, with the superscript being called the transpose.
and call it a row vector, with the superscript being called the transpose.  , xn), y (y1,
, xn), y (y1,  , yn) R n, we write
, yn) R n, we write 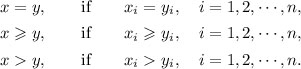 Note that when n = 1, for any x, y R , one must have
Note that when n = 1, for any x, y R , one must have